Test psychotechnique (Suite)
Test psychotechnique (Suite)
Test de logique numérique
Les tests de logique numérique sont conçus pour évaluer les capacités d'une personne à raisonner avec les chiffres et à calculer mentalement.
Ces tests suivent les mêmes principes que ceux des tests de séries numériques. Le but est donc de retrouver la règle de logique afin de déterminer les nombres manquants.
Test de recherche d'intrus
Dans le test de recherche d'intrus, il faut identifier le point commun à tous les éléments d'un groupe afin d'exclure celui qui est différent des autres.
Ainsi, contrairement aux tests des séries, il ne faut pas chercher à identifier une logique de progression mais analyser les éléments afin de repérer une similitude ou une différence entre chaque élément.
Ce type de test fait appel à l'esprit d'observation, d'analyse et de déduction du candidat.
Les règles d'exclusion sont nombreuses, nous vous listons ci-dessous celles les plus fréquemment rencontrées.
Parité
Nombres pairs : 0 2 4 6 8 10 ...
Nombres impairs : 1 3 5 7 9 11 ...
Exemple :
Nombres pairs : 0 2 4 6 8 10 ...
Nombres impairs : 1 3 5 7 9 11 ...
Exemple :
Trouvez l'intrus 12 68 91 54 20
Solution : 91 est le seul nombre impair dans la liste
Solution : 91 est le seul nombre impair dans la liste
Nombres premiers
Nombres premiers : 2 3 5 7 11 13 17 19 23 ...
Exemple :
Trouvez l'intrus 5 7 17 21 23
Solution : 21 n'est pas un nombre premier (divisible par 7 et 3)
Multiples et diviseurs communs
Multiples de 3 : 0 3 9 12 15 18 ...
Divisible par 11 : 121 165 176 ...
Exemple :
Nombres premiers : 2 3 5 7 11 13 17 19 23 ...
Exemple :
Trouvez l'intrus 5 7 17 21 23
Solution : 21 n'est pas un nombre premier (divisible par 7 et 3)
Multiples et diviseurs communs
Multiples de 3 : 0 3 9 12 15 18 ...
Divisible par 11 : 121 165 176 ...
Exemple :
Trouvez l'intrus 48 56 84 91 105
Solution : 48 n'est pas divisible par 7
Puissance
Carré parfait : 0 1 4 9 16 25 36 49 64 81 100 121 ...
Puissance
Carré parfait : 0 1 4 9 16 25 36 49 64 81 100 121 ...
Cube parfait : 0 1 8 27 64 125 216 343 512 729 ...
Exemple :
Trouvez l'intrus 27 125 512 624
Solution : 624 n'est pas un cube parfait
Calcul entre les chiffres
Exemple :
Trouvez l'intrus 132 453 363 286
Calcul entre les chiffres
Exemple :
Trouvez l'intrus 132 453 363 286
Solution : 453 est le seul nombre dont la somme des deux chiffres extérieurs n'est pas égale au chiffre central
Exemple :
Trouvez l'intrus 5016 3159 5027 5231
Exemple :
Trouvez l'intrus 5016 3159 5027 5231
Solution : 5231 est le seul nombre dont la somme des trois premiers chiffres n'est pas égale au dernier chiffre
Exemple :
Trouvez l'intrus 24 46 36 12 48 Solution : 46 est le seul nombre dont le chiffre des unités n'est pas égal au double du chiffre des dizaines
Exemple :
Trouvez l'intrus 55 46 28 19 27
Exemple :
Trouvez l'intrus 24 46 36 12 48 Solution : 46 est le seul nombre dont le chiffre des unités n'est pas égal au double du chiffre des dizaines
Exemple :
Trouvez l'intrus 55 46 28 19 27
Solution : 27 est le seul nombre dont la somme des chiffres n'est pas égale à 10
Exemple :
Trouvez l'intrus 253 829 627 258 516
Exemple :
Trouvez l'intrus 253 829 627 258 516
Solution : 258 est le seul nombre dont le chiffre des unités n'est pas égal à +1 du chiffre des centaines
Observation
Exemple :
Trouvez l'intrus 515 247 651 157
Exemple :
Trouvez l'intrus 515 247 651 157
Solution : 515 est le seul nombre qui n'a pas 3 chiffres différents
Exemple :
Trouvez l'intrus 5125 2792 6526 1284
Exemple :
Trouvez l'intrus 5125 2792 6526 1284
Solution : 1284 est le seul nombre qui n'a pas le même chiffre pour les chiffres des unités et des milles
Exemple :
Trouvez l'intrus 2345 6789 4567 5689
Solution : 5689 est le seul nombre qui n'a pas 4 chiffres consécutifs
Exemple :
Trouvez l'intrus 2345 6789 4567 5689
Solution : 5689 est le seul nombre qui n'a pas 4 chiffres consécutifs
Test de recherche d'intrus lettre
Dans le test de l'intrus, il faut analyser plusieurs groupes de lettres afin d'identifier leur point commun et ainsi pouvoir exclure celui qui est différent des autres.
Ce test nécessite de la part du candidat un esprit d'observation, d'analyse et de déduction.
Les règles d'exclusion sont nombreuses, nous vous listons ci-dessous celles les plus fréquemment rencontrées.
Dans le test de l'intrus, il faut analyser plusieurs groupes de lettres afin d'identifier leur point commun et ainsi pouvoir exclure celui qui est différent des autres.
Ce test nécessite de la part du candidat un esprit d'observation, d'analyse et de déduction.
Les règles d'exclusion sont nombreuses, nous vous listons ci-dessous celles les plus fréquemment rencontrées.
Règle générale
Les groupes de lettres sont très souvent construits à partir d'une logique liée à leur rang dans l'alphabet. Il est donc recommandé de se noter l'alphabet numéroté en ordre croissant et décroissant. Il devient ainsi rapide de déterminer le rang de chaque lettre et d'éliminer le groupe de lettres qui ne répond pas à la même règle que les autres.
Suite de lettres
A B C D E F G H I J 1
262
253
244
235
226
217
208
199
1810
17
K L M N O P Q R S T 11
1612
1513
1414
1315
1216
1117
1018
919
820
7
U V W X Y Z 21
622
523
424
325
226
1
Exemple :
Trouvez l'intrus DE MN IK WX
Solution : IK, ce groupe de lettres n'est pas formé de deux lettres consécutives
D[4]E[5] M[13]N[14] I[9]K[11] W[23]X[24]
Exemple :
Trouvez l'intrus FI PR KN UX
D[4]E[5] M[13]N[14] I[9]K[11] W[23]X[24]
Exemple :
Trouvez l'intrus FI PR KN UX
Solution : PR, ce groupe de lettres n'a qu'une lettre au lieu de deux entre les deux éléments
F[6]I[9] P[16]R[18] K[11]N[14] U[21]X[24]
Lettres opposées
Exemple :
Trouvez l'intrus AZ EV MN BX
F[6]I[9] P[16]R[18] K[11]N[14] U[21]X[24]
Lettres opposées
Exemple :
Trouvez l'intrus AZ EV MN BX
Solution : BX, ce groupe de lettres n'est pas formé de deux lettres ayant des rangs opposés (ce qui revient à avoir la somme des rangs égale à 27)
A[1]Z[26] E[5]V[22] M[13]N[14] B[2]X[24]
Répétition de lettres
Exemple :
Trouvez l'intrus DPLP QJUQ EVIR DHDM
A[1]Z[26] E[5]V[22] M[13]N[14] B[2]X[24]
Répétition de lettres
Exemple :
Trouvez l'intrus DPLP QJUQ EVIR DHDM
Solution : EVIR, ce groupe de lettres est le seul à avoir 4 lettres différentes
Exemple :
Trouvez l'intrus HAXRP RJXOA BKFMW FURAX
Exemple :
Trouvez l'intrus HAXRP RJXOA BKFMW FURAX
Solution : BKFMW, ce groupe de lettres est le seul à ne pas contenir les lettres ARX
Voyelle - Consonne
Exemple :
Trouvez l'intrus CHB PGX TVZ YGS
Voyelle - Consonne
Exemple :
Trouvez l'intrus CHB PGX TVZ YGS
Solution : YGS, ce groupe de lettres est le seul à avoir une voyelle
Majuscule - Minuscule
Exemple :
Trouvez l'intrus Rio FZe fDI yuR Solution : fDI, ce groupe de lettres ne respecte pas la règle d'écriture : les voyelles en minuscule et les consonnes en majuscule
Opération à partir des rangs
Exemple :
Trouvez l'intrus ADE GMO DJN XBZ
Majuscule - Minuscule
Exemple :
Trouvez l'intrus Rio FZe fDI yuR Solution : fDI, ce groupe de lettres ne respecte pas la règle d'écriture : les voyelles en minuscule et les consonnes en majuscule
Opération à partir des rangs
Exemple :
Trouvez l'intrus ADE GMO DJN XBZ
Solution : GMO, la somme des rangs des deux premières lettres est égale au rang de la troisième lettre du groupe
A[1]+D[4]=E[5] G[7]+M[13]≠O[15] D[4]+J[10]=N[14] X[24]+B[2]=Z[26]
Test de recherche d'intrus graphique
Dans le test de recherche d'intrus graphique, il faut retrouver la relation qui existe entre plusieurs figures et ainsi pouvoir exclure celle qui est différente.
A noter qu'il faut observer les figures indépendamment les unes des autres. En effet, il ne s'agit pas de chercher une progression entre elles mais bien un point commun.
A[1]+D[4]=E[5] G[7]+M[13]≠O[15] D[4]+J[10]=N[14] X[24]+B[2]=Z[26]
Test de recherche d'intrus graphique
Dans le test de recherche d'intrus graphique, il faut retrouver la relation qui existe entre plusieurs figures et ainsi pouvoir exclure celle qui est différente.
A noter qu'il faut observer les figures indépendamment les unes des autres. En effet, il ne s'agit pas de chercher une progression entre elles mais bien un point commun.
Questions les plus fréquentes
Dans ce type de test, certaines règles de logique reviennent régulièrement. Nous vous listons ci-dessous celles les plus fréquemment rencontrées.
Nombre d'éléments
Exemple :
Quel est l'intrus?

Solution : Dans chaque figure, sauf la n°4, il y a un élément répété 3 fois et un autre 1 fois.
Exemple :
Quel est l'intrus?

Solution : Dans chaque figure, sauf la n°2, le nombre de ronds est impair.
Nombre de parts
Exemple :
Quel est l'intrus?
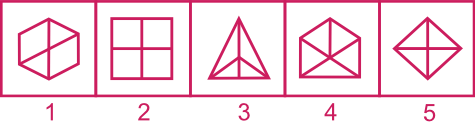
Solution : Chaque figure, sauf la n°4, est divisée en 4 parts.
Exemple :
Quel est l'intrus?
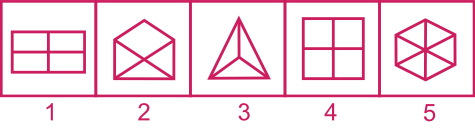
Solution : Dans chaque figure, sauf la n°2, le nombre de parts est égal au nombre de côtés de la forme.
Exemple :
Quel est l'intrus?
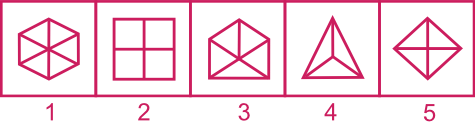
Solution : Dans chaque figure, sauf la n°3, chaque part a la même surface.
Nombre de côtés
Exemple :
Quel est l'intrus?

Solution : Chaque figure, sauf la n°1, a 4 côtés.
Exemple :
Quel est l'intrus?

Solution : Dans chaque figure, sauf la n°2, la forme du haut a un côté de plus que la forme du bas.
Nombre de traits
Exemple :
Quel est l'intrus?

Solution : Chaque figure, sauf la n°5, a 5 traits.
Orientation - Direction
Exemple :
Quel est l'intrus?

Solution : Dans chaque figure, sauf la n°1, les triangles ont des directions opposées.
Exemple :
Quel est l'intrus?

Solution : Dans chaque figure, sauf la n°4, le trait part d'un angle pour traverser le côté opposé.
Symétrie - Rotation
Exemple :
Quel est l'intrus?
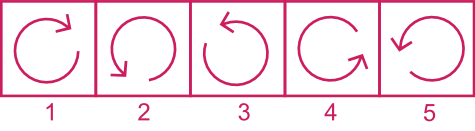
Solution : Chaque figure, sauf la n°1, est identique, il suffit de les faire pivoter pour les superposer.
Exemple :
Quel est l'intrus?

Solution : Dans chaque figure, sauf la n°4, le trait représente un axe de symétrie.
Analogie visuelle
Les tests d'analogie visuelle (ou encore appelés tests d'analogie graphique) sont construits sur le même raisonnement que ceux des tests d'analogie verbale du type : A est à B, ce que C est à D.
Ainsi, il faut chercher la transformation subit par la figure A pour obtenir la B, afin de l'appliquer à la figure C et ainsi déterminer la nouvelle figure D.
Les types de tests d'analogie visuelle
Il existe plusieurs types de représentation pour ce genre de test.
1er type : Choisir un élément d'une paire
Exemple :
Quel est l'intrus?

Solution : Dans chaque figure, sauf la n°4, il y a un élément répété 3 fois et un autre 1 fois.
Exemple :
Quel est l'intrus?

Solution : Dans chaque figure, sauf la n°2, le nombre de ronds est impair.
Nombre de parts
Exemple :
Quel est l'intrus?

Solution : Chaque figure, sauf la n°4, est divisée en 4 parts.
Exemple :
Quel est l'intrus?

Solution : Dans chaque figure, sauf la n°2, le nombre de parts est égal au nombre de côtés de la forme.
Exemple :
Quel est l'intrus?

Solution : Dans chaque figure, sauf la n°3, chaque part a la même surface.
Nombre de côtés
Exemple :
Quel est l'intrus?

Solution : Chaque figure, sauf la n°1, a 4 côtés.
Exemple :
Quel est l'intrus?

Solution : Dans chaque figure, sauf la n°2, la forme du haut a un côté de plus que la forme du bas.
Nombre de traits
Exemple :
Quel est l'intrus?

Solution : Chaque figure, sauf la n°5, a 5 traits.
Orientation - Direction
Exemple :
Quel est l'intrus?

Solution : Dans chaque figure, sauf la n°1, les triangles ont des directions opposées.
Exemple :
Quel est l'intrus?

Solution : Dans chaque figure, sauf la n°4, le trait part d'un angle pour traverser le côté opposé.
Symétrie - Rotation
Exemple :
Quel est l'intrus?

Solution : Chaque figure, sauf la n°1, est identique, il suffit de les faire pivoter pour les superposer.
Exemple :
Quel est l'intrus?

Solution : Dans chaque figure, sauf la n°4, le trait représente un axe de symétrie.
Analogie visuelle
Les tests d'analogie visuelle (ou encore appelés tests d'analogie graphique) sont construits sur le même raisonnement que ceux des tests d'analogie verbale du type : A est à B, ce que C est à D.
Ainsi, il faut chercher la transformation subit par la figure A pour obtenir la B, afin de l'appliquer à la figure C et ainsi déterminer la nouvelle figure D.
Les types de tests d'analogie visuelle
Il existe plusieurs types de représentation pour ce genre de test.
1er type : Choisir un élément d'une paire
Solution 1 :

Solution 1 :


Solution 1 :
Solution 1 :


2ème type : Choisir une paire
Exemple :


 Réponse : 1
Réponse : 13ème type : Choisir un élément dans chaque paire
Exemple :


 Réponse : 1
Réponse : 14ème type : Choisir l'intrus parmi les paires
Exemple :

 Réponse : 1
Réponse : 1
Les transformations les plus fréquentes
Déplacement
Déplacement en diagonale

Déplacement vertical (haut en bas ou inversement)

Déplacement horizontal (gauche à droite ou inversement)

Rotation
Rotation de 45° dans le sens horaire

Rotation de 90° dans le sens horaire

Rotation de 135° dans le sens horaire

Rotation de 180°

Rotation de 135° dans le sens anti-horaire

Rotation de 90° dans le sens anti-horaire

Rotation de 45° dans le sens anti-horaire

Symétrie
Symétrie axe vertical

Symétrie axe horizontal
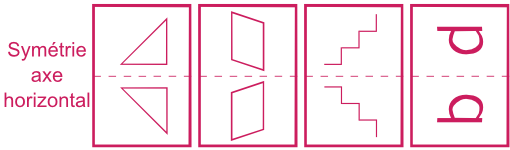
Changement de couleur

Changement de forme

Multiplication du nombre d'éléments

Les principales priorités d'un cube à connaître pour réussir les tests de cube sont listées ci-dessous.
Un cube à 6 faces

Seulement 3 faces sont visibles en même temps

Règle 1 : Deux faces opposées ne peuvent pas être adjacentes les unes aux autres
Les faces visibles ne peuvent jamais être en opposition l'une de l'autre.
Exemple :
Quelle lettre est à l'opposé de la lettre A?
 Réponse : la lettre C. En sachant que les 3 faces visibles ne peuvent pas être opposées, les figures 1 et 2 nous permettent d'éliminer les lettres B, D et E. La figure 3 nous confirme que la lettre opposée à A est C.
Réponse : la lettre C. En sachant que les 3 faces visibles ne peuvent pas être opposées, les figures 1 et 2 nous permettent d'éliminer les lettres B, D et E. La figure 3 nous confirme que la lettre opposée à A est C.
Règle 2 : Si pour 2 dés, 2 faces sont adjacentes et l'une des 2 faces est à la même position, alors les 2 autres faces visibles sont opposées
Exemple :
Quelle lettre est à l'opposé de la lettre B?
 Réponse : la lettre D. Les lettres A et E sont adjacentes sur les deux cubes et E est à la même position, ainsi les deux autres lettres sont forcément opposées.
Réponse : la lettre D. Les lettres A et E sont adjacentes sur les deux cubes et E est à la même position, ainsi les deux autres lettres sont forcément opposées.
Règle 3 : Si sur 2 dés une seule face est commune et à la même position, alors les faces opposées ont la même position
Exemple :
Quelle lettre est à l'opposé de la lettre B?
 Réponse : la lettre D. La lettre A est commune et à la même position sur les 2 dés, ainsi la lettre B est opposée à la lettre D (et C à E).
Réponse : la lettre D. La lettre A est commune et à la même position sur les 2 dés, ainsi la lettre B est opposée à la lettre D (et C à E).
Il existe 11 patrons du cube
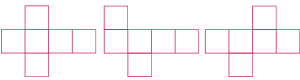


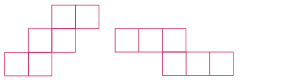
L'analyse du patron permet de trouver rapidement le cube qui en résulte.
Exemple 1 :

Sur ce patron, nous avons 1 opposé à 6, 2 à 5, 3 à 4.
Exemple 2 :
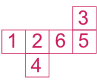
Sur ce patron, nous avons 1 opposé à 6, 2 à 5, 3 à 4.
Exemple 3 :
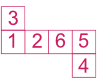
Sur ce patron, nous avons 1 opposé à 6, 2 à 5, 3 à 4.
Exemple 4 :
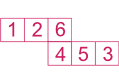
Sur ce patron, nous avons 1 opposé à 6, 2 à 5, 3 à 4.
L'addition du nombre de points (ou chiffres) des faces opposées d'un dé standard est toujours égale à 7. De plus, la somme de deux faces adjacentes ne peut pas être égale à 7.
Exemple :
Quelle chiffre est à l'opposé du 1?
 Réponse : le chiffre 6.
Réponse : le chiffre 6.
Nous constatons que la somme de deux faces adjacentes n'est jamais égale à 7.

Si nous découpons ce cube en X parts (ici X = 3), nous obtenons différents types de cubes :
Cubes centraux :
1 seule face visible (représentée par une croix).
Nombre de cubes centraux = 6 (X-2)2 = 6 (3-2)2 = 6
Cubes au milieu :
2 faces visibles (représentées en blanc).
Nombre de cubes au milieu = 12 (X-2) = 12 (3-2) = 12
Cubes au coin :
3 faces visibles (représentées en couleur).
Nombre de cubes au coin = 8 (toujours égal à 8)
Cubes au centre :
0 face visible.
Nombre de cubes au centre = (X-2)3 = 1
Le nombre total de cubes est obtenu par la formule: X3 = 27
Les figures ci-dessous montrent l'empilement de cubes sur plusieurs étages :
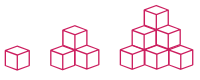
Pour 1 étage, nous avons 1 cube, pour 2 étages 4 cubes, pour 3 étages 10 cubes.
Pour les compter facilement, nous vous conseillons de le faire par colonne en plaçant votre regard de côté. Par exemple, pour la dernière figure, nous obtenons 6 + 3 + 1 = 10.
Un autre exemple d'empilement :

Pour 1 étage, nous avons 1 cube, pour 2 étages 5 cubes, pour 3 étages 14 cubes.
Pour les compter facilement, nous vous conseillons de le faire par ligne en plaçant votre regard de face. Par exemple, pour la dernière figure, nous obtenons 1 + 4 + 9 = 14.
Dans certains exercices, vous devrez compter le nombre de faces d'une structure.
Exemple :
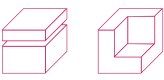 Réponses : 12 et 9.
Réponses : 12 et 9.
Dans le test des opérateurs, une forme est désignée par une lettre. Si celle-ci est accompagnée d'un sigle, elle subit une transformation qu'il faut identifier (changement de couleur, de taille, de position ...).
Exemple :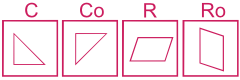
Le sigle o indique que la forme subit une rotation de 90° dans le sens horaire.
Exemple de question:
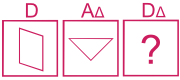
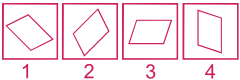 Le sigle Δ indique que la forme subit une rotation de 45° dans le sens anti-horaire; la bonne réponse est la n°1.
Le sigle Δ indique que la forme subit une rotation de 45° dans le sens anti-horaire; la bonne réponse est la n°1.
Le test des opérations codées consiste à résoudre un système d'équations à partir de symboles.
Exemple : ◍ = ▢ + 2 ◍ = ▢ + ▢ Il est plus facile de résoudre le système en remplaçant les symboles par des lettres. x = y + 2 x = y + y = 2 y Méthode par substitution : une inconnue est exprimée en fonction de l'autre puis elle est remplacée dans la seconde équation. x = 2 y = y + 2 y = 2 et x = 4 y = 2 Ainsi : ◍ = 4 et ▢ = 2
Le but des tests des tableaux codés est de retrouver la valeur de symboles regroupés dans une grille à partir d'opérations fournies afin de résoudre une nouvelle opération.
Les règles logiques sont nombreuses, il convient d'observer l'agencement des symboles et d'y retrouver par exemple une symétrie, une progression horizontale ou verticale, une opération en ligne ou en colonne ...
Exemple :
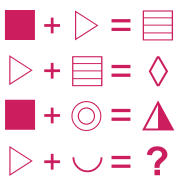 Réponse :
Réponse : 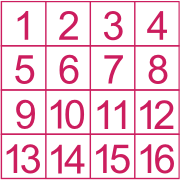
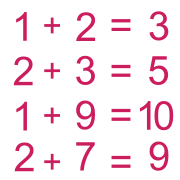
Dans le test de substitution, les lettres d'un mot ou d'une phrase sont remplacées par exemple par des chiffres. Il faut retrouver le code de substitution afin de déterminer le mot ou la phrase qui correspond au codage.
Exemple : Quel est le mot codé? 1 18 2 18 5 Réponse : Le mot est A R B R E, les chiffres correspondent au rang des lettres dans l'alphabet.
Pour commencer ce genre de test, il est important de se noter l'alphabet numéroté en ordre croissant et décroissant. En effet, de nombreuses questions utilisent le rang des lettres dans l'alphabet.
A
B
C
D
E
F
G
H
I
J
1
26
2
25
3
24
4
23
5
22
6
21
7
20
8
19
9
18
10
17
K
L
M
N
O
P
Q
R
S
T
11
16
12
15
13
14
14
13
15
12
16
11
17
10
18
9
19
8
20
7
U
V
W
X
Y
Z
21
6
22
5
23
4
24
3
25
2
26
1
A partir du tableau, il devient facile de remplacer les lettres par leur numéro d'ordre et de retrouver la logique de progression.
Type 1 - Test de substitution avec indice
Exemple 1 : Si B S C S F correspond à A R B R E alors à quoi correspond T B Q J O?
Réponse : S A P I N, chaque lettre est remplacée par celle qui la succède dans l'ordre alphabétique.
Exemple 2 : Si 1 18 2 18 5 correspond à A R B R E alors à quoi correspond 19 1 16 9 14?
Réponse : S A P I N, chaque lettre est remplacée par son rang dans l'alphabet.
Type 2 - Test de substitution sans indice
Ce type de test de substitution est plus difficile car il fait appel à votre sens de la perspicacité.
Pour trouver la logique de codage, vous devez commencer par repérer les lettres isolées qui sont A ou Y, les apostrophes qui sont toujours suivies d'une voyelle, les lettres les plus fréquentes dans la langue française : E, S, A, I, T et enfin les petits mots qui sont souvent des articles (le, la, de, ...).
Exemple : 18 - 7 - 22 - 11 - 22 3 18 - 7 - 22 - 11 - 22 14 ' 17 - 11 - 21 - 7 - 3 - 23 8 - 3 - 11 - 22 21 - 17 - 16 16 - 11 - 6 Réponse : le chiffre 3 correspond à une lettre isolée et est donc forcément A ou Y. Comme le chiffre est répété dans plusieurs mots, nous supposons que 3 = A.
Le chiffre 17 est derrière une apostrophe, ainsi il correspond à une voyelle. Entre 17 et 3, il y a 14 rangs qui les séparent; ainsi à partir de l'alphabet nous en déduisons que 17 = O.
Ainsi, nous trouvons la logique de codage : le chiffre correspond au rang de la lettre dans l'alphabet + 2.
PETIT A PETIT L ' OISEAU FAIT SON NID
Les tests d'orientation évaluent vos capacités à vous déplacer dans l'espace.
Les ordres peuvent être donnés de plusieux façons :
- à l'aide des points cardinaux Nord - Est - Sud - Ouest (par exemple : direction Sud-Est)

- par des directions en degrés
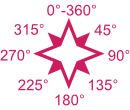
- par des changements de cap exprimés en heure (par exemple : cap à 3 heure, soit un changement de direction de 90° dans le sens horaire par rapport à la direction initiale).
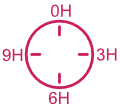
Test de la boussole type pilote
Le test de la boussole nécessite de suivre des instructions afin de trouver une direction finale.
Exemple 1 : Question 1 : Un coureur oriente sa boussole au nord et se dirige comme indiqué ci-dessous. Quelle est sa direction? Réponse 1 : Il suffit de compléter les points cardinaux pour connaître la direction du coureur :
Réponse 1 : Il suffit de compléter les points cardinaux pour connaître la direction du coureur :  Il se dirige vers l'ouest. Question 2 : Puis, il suit les changements de direction suivants : cap à 3 heures puis cap à 6 heures. Quelle est sa direction finale? Réponse 2 : Cap à 3 heures : il pivote de 90° dans le sens horaire par rapport à sa position initiale, il se dirige maintenant vers le nord.
Il se dirige vers l'ouest. Question 2 : Puis, il suit les changements de direction suivants : cap à 3 heures puis cap à 6 heures. Quelle est sa direction finale? Réponse 2 : Cap à 3 heures : il pivote de 90° dans le sens horaire par rapport à sa position initiale, il se dirige maintenant vers le nord.  Cap à 6 heures : il pivote de 180°, il fait un demi tour, il se dirige maintenant vers le sud.
Cap à 6 heures : il pivote de 180°, il fait un demi tour, il se dirige maintenant vers le sud.  Il se dirige donc vers le sud.
Il se dirige donc vers le sud.
Exemple 2 : Question 1 : Un nageur oriente sa boussole au nord et se dirige comme indiqué ci-dessous. Après 5 minutes de nage, cap au nord. Puis, après 10 minutes, cap à 6 heures. Puis, après 5 minutes, cap à 3 heures pendant 5 minutes. Combien de temps le nageur se dirige-t-il vers le nord? Réponse : Le nageur commence par 5 minutes vers l'est.
Réponse : Le nageur commence par 5 minutes vers l'est.  Puis il se dirige au nord pendant 10 minutes.
Puis il se dirige au nord pendant 10 minutes.  Puis cap à 6 heures, ce qu'il signifie qu'il fait demi-tour, il se dirige donc au sud pendant 5 minutes.
Puis cap à 6 heures, ce qu'il signifie qu'il fait demi-tour, il se dirige donc au sud pendant 5 minutes.  Puis cap à 3 heures, ce qu'il signifie qu'il fait 90° dans le sens horaire par rapport à sa direction actuelle, il se dirige donc à l'ouest pendant 5 minutes.
Puis cap à 3 heures, ce qu'il signifie qu'il fait 90° dans le sens horaire par rapport à sa direction actuelle, il se dirige donc à l'ouest pendant 5 minutes.  Le nageur se dirige donc 10 minutes vers le nord
Le nageur se dirige donc 10 minutes vers le nord
Le test de déplacement dans une grille nécessite de suivre des instructions afin de trouver la case finale.
Exemple : Il faut se déplacer dans la grille en suivant les instructions suivantes : 2N-3O-1SE.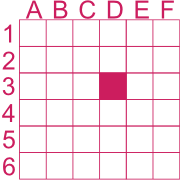
 Réponse : L'instruction 2N-3O-1SE, signifie qu'il faut aller 2 cases vers le nord puis 3 cases vers l'ouest et enfin 1 case vers le sud-est. Grâce à la boussole, nous déduisons les directions à prendre.
Réponse : L'instruction 2N-3O-1SE, signifie qu'il faut aller 2 cases vers le nord puis 3 cases vers l'ouest et enfin 1 case vers le sud-est. Grâce à la boussole, nous déduisons les directions à prendre. 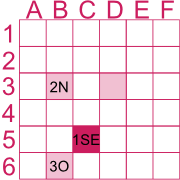

La case finale est C5.
Le but des tests de pliage découpé est de trouver la figure qui est formée lorsqu'une feuille pliée est découpée puis de nouveau dépliée.
Exemple :

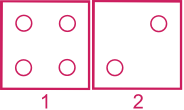
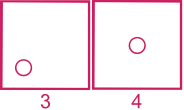 Réponse : 1
Réponse : 1
Le test de logique déductive consiste à établir une conclusion à partir d'un ensemble d'hypothèses.
Ainsi, dans le test des positions logiques, il faut retrouver la position d'un objet à partir d'une série d'affirmations. La disposition des éléments peut être linéaire (exemple: aligné en rang) ou encore circulaire (exemple: assis autour d'une table).
Direction
- Lorsque la direction n'est pas mentionnée, il faut orienter la figure ainsi :

A est juste à gauche de B
A, B, C, D sont à gauche de E
C est juste à droite de B
C, D, E sont à droite de B
- Lorsque la direction est indiquée vers vous, il faut orienter la figure ainsi :

A est juste à droite de B
A, B, C, D sont à droite de E
C est juste à gauche de B
C, D, E sont à gauche de B
- Lorsqu'il y a deux lignes, les directions peuvent être différentes en fonction de la ligne:

A est juste à droite de B
A, B sont à droite de C
A est à l'opposé de D
A est diagonalement opposé à F
B est à l'opposé de E
D est juste à gauche de E
D, E sont à gauche de F
Règles
Règle 1

Si A est à côté de B, alors il y a 2 cas possibles :
- A est sur le côté gauche de B (cas 1)
- A est sur le côté droit de B (cas 2)
Règle 2

Si B est assis entre A et C, alors il y a 2 cas possibles :
- A est sur le côté gauche de B et C sur le côté droit de B (cas 1)
- A est sur le côté droit de B et C sur le côté gauche de B (cas 2)
Exemple Lisez attentivement ces informations :
- 5 élèves sont assis en ligne face au nord
- Marc est juste à gauche d'Anne
- Julie est entre Pierre et Sophie
- Sophie est entre Marc et Julie
Qui est au centre? Réponse D'après l'énoncé, nous savons :
- 5 élèves sont assis en ligne face au nord

- Marc est juste à gauche d'Anne

- Julie est entre Pierre et Sophie

- Sophie est entre Marc et Julie

A partir de ces éléments, nous pouvons déduire que Sophie est assise au milieu.

Le but est de retrouver la position d'éléments ou de personnes répartis de façon circulaire. Ils peuvent être disposés autour d'une table ronde ou rectangulaire ou de tout autre arrangement en boucle fermée.
Direction
- Les objets ou personnes peuvent être orientés face au centre :

A est juste à droite de B
A, D sont à droite de B
A est à l'opposé de C
C est juste à droite de D
- Les objets ou personnes peuvent être orientés dos au centre :

A est juste à gauche de B
A, B sont à droite de D
C est juste à droite de B
B est à l'opposé de D
Règles
Les règles sont les mêmes que celles des arrangements linéaires.
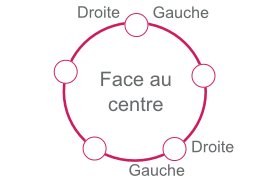
Exemple Lisez attentivement ces informations :
- 5 élèves sont assis face à face autour d'une table
- Marc est juste à gauche d'Anne
- Julie est entre Pierre et Sophie
- Sophie est entre Marc et Julie
Qui est à droite d'Anne? Réponse D'après l'énoncé, nous savons :
- 5 élèves sont assis en ligne face au nord
- Marc est juste à gauche d'Anne

- Julie est entre Pierre et Sophie

- Sophie est entre Marc et Julie

A partir de ces éléments, nous pouvons déduire que Pierre est assis à droite d'Anne.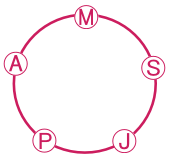
Dans certaines questions de logique, il faudra identifier les liens de parenté qui existent entre plusieurs individus, c'est à dire la relation qui les lie entre eux.
Pour se préparer à ce type de test, il est indispensable de connaître certaines expressions que nous vous listons ci-dessous.
Lien de parenté direct
Dans ce type d'exercice, il faut retrouver la relation qui lie deux personnes directement.
Pour cela, il faut décomposer la phrase en partant de la fin de l'énoncé et en remontant jusqu'au verbe.
Exemple :
En montrant Marc, Sophie dit : "il est le fils de la fille unique du mari de ma mère".
Quel est le lien entre Marc et Sophie?
Solution :
En partant de la fin de la phrase:
- le mari de ma mère = son père (hypothèse)
- la fille unique de son père = elle-même (Sophie)
- le fils de Sophie = son fils
Marc est le fils de Sophie A noter que nous sommes obligés de supposer que le "mari de sa mère" soit son père. Pour valider l'hypothèse, il faut écarter les autres réponses proposées.
Exemple :
En discutant de Faustine, Florian dit : "elle est l'unique fille de la mère de mon frère".
Quel est le lien entre Faustine et Florian?
Solution :
En partant de la fin de la phrase:
- la mère de mon frère = ma mère
- l'unique fille de ma mère = ma soeur
Faustine est la soeur de Florian
Lien de parenté indirect
Dans ce type d'exercice, il faut retrouver la relation qui lie deux personnes indirectement.
Pour cela, il faut décomposer la phrase en deux parties; tout d'abord en partant de la fin de l'énoncé et en remontant jusqu'au verbe et ensuite en partant du sujet de la phrase jusqu'au verbe.
Exemple :
En montrant Antoine, Marie dit : "la mère de sa soeur est la fille unique de ma grand-mère".
Quel est le lien entre Antoine et Marie?
Solution :
En partant de la fin de la phrase:
- la fille unique de ma grand-mère = la mère de Marie
En partant du début de la phrase:
- la mère de sa soeur = la mère d'Antoine
Ainsi, la mère d'Antoine est la mère de Marie, donc Antoine est le frère de Marie.
Exemple :
En introduisant Pierre, Lucie dit : "la seule fille de sa mère est ma mère".
Quel est le lien entre Pierre et Lucie?
Solution :
En partant de la fin de la phrase:
- ma mère = la mère de Lucie
En partant du début de la phrase:
- la seule fille de sa mère = la soeur de Pierre
Ainsi, la soeur de Pierre est la mère de Lucie, donc Pierre est l'oncle de Lucie
Dans ce type d'exercice, il faut retrouver les relations qui lient plusieurs personnes.
Pour cela, il faut décomposer la phrase en essayant par exemple de créer un arbre généalogique.
Exemple :
A et B sont soeurs. C et D sont frères. La fille de A est la soeur de D.
Quel est le lien entre B et C? Solution : La fille de A est la soeur de D donc A est la mère de C et D ainsi B, qui est la soeur de A, est la tante de C.
Exemple :
A et B sont mariés. C et D sont frères. A est la soeur de C.
Quel est le lien entre B et D? Solution : A est la soeur de C donc A, C et D sont frères et soeur ainsi B, qui est le mari de A, est le beau-frère de D.
Dans ce type d'exercice, les relations qui lient plusieurs personnes sont codées par des symboles comme + - x / etc..
Exemple :
On sait que : A + B signifie que A est la soeur de B A - B signifie que A est le frère de B A x B signifie que A est la fille de B
Quelle est l'équation qui montre que C est l'oncle maternel de D? a) E - C + D b) D + E - C c) D x E + C d) E x D + C
Solution : Réponse c) C est l'oncle maternel de D
donc C est le frère de la mère de D
ou D est la fille de la soeur de C
ainsi si la mère = E, nous avons D x E + C
Nous pouvons vérifier facilement cette réponse : D x E + C = D "est la fille de" E "qui est la soeur de" C
Pour les autres propositions a) E - C + D : E "est le frère de" C "qui est la soeur de" D soit C est la soeur de D b) D + E - C : D "est la soeur de" E "qui est le frère de" C soit C est la soeur (ou le frère?) de D d) E x D + C : E "est la fille de" D "qui est la soeur de" C soit C est la tante de ETEST MATHEMATIQUE
Les tests de raisonnement mécanique sont conçus pour évaluer vos connaissances techniques, mécaniques et physiques. Ils contiennent généralement des questions qui ne nécessitent pas de connaissances particulières, mais qui font appel à votre sens physique.
Les notions physiques régulièrement présentent dans ce genre de tests sont l'électricité, la mécanique (par exemple les balances, les leviers, les engrenages, les manivelles et les poulies), les structures (par exemple les effets de la compression), l'énergie (par exemple la transmission de la chaleur, la lumière et la puissance), les forces (par exemple la pesanteur, les effets de rotation, comme la force centrifuge).
Un circuit électrique comprend : une source électrique (exemple: batterie, prise électrique), du fil électrique, un appareil électrique et un interrupteur (option) pour controler le circuit.
Symboles
Interrupteur :

Ampoule :

Batterie :

Prise :

Deux fils connectés :

Deux fils non connectés :

Fusible :

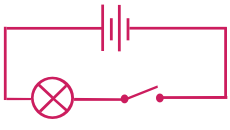
Pour fonctionner, un circuit a besoin d'être fermé, c'est à dire que toutes les parties du circuit doivent être connectées.
Exemple :

L'interrupteur est ouvert, le circuit n'est pas fermé, la lampe ne s'allume pas.

L'interrupteur est fermé, le circuit est fermé, la lampe s'allume.
Circuit en série - parallèle
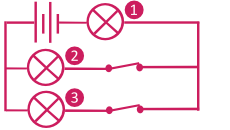
La lampe 1 est en série alors que les lampes 2 et 3 sont installées en parallèle.
Si la lampe 1 est supprimée, le circuit est ouvert, toutes les lampes s'éteignent.
Si la lampe 2 est supprimée (ou la lampe 3), le circuit reste fermé, les autres lampes restent allumées.
Court circuit

L'interrupteur crée un chemin préférentiel pour l'électricité car il y a moins de résistance que le chemin avec l'ampoule. Ainsi, l'électricité passe par l'interrupteur et l'ampoule s'éteint quand l'interrupteur ferme le circuit.

Pour le cicuit 2, le cable supplémentaire court circuite le circuit, la lampe reste éteinte. Pour le circuit 1, le cable supplémentaire n'a pas d'incidence, la lampe reste allumée.
Connexion de batteries
Série

La lampe s'allume.

La lampe ne s'allume pas.
Parallèle

La lampe s'allume.
La gravité est la loi physique qui explique l'attraction terrestre des corps. Cette force est verticale et dirigée vers le centre de la Terre.
Exemple :

Sachant que l'ensemble est à l'arrêt, la boule sera dirigée comme sur la figure 1. En effet, la gravité dirige la boule verticalement.
Vitesse et temps de chute d'un objet
La vitesse de chute d'un objet dans le vide ne dépend pas de son poids (en considérant que la force de résistance de l'air est négligeable). Ainsi, une bille en fer tombera à la même vitesse qu'une bille en plastique.
De plus, la durée de la chute est fonction uniquement de la hauteur de la chute et est indépendante de la masse.
Exemple :

Les deux balles tombent de la même hauteur, elles toucheront le sol en même temps.
Pendule

Le pendule doit son mouvement oscillatoire à l'effet de la pesanteur. Au bout d'un fil inextensible, une petite masse est accrochée. En écartant celle-ci de sa position d'équilibre, elle oscille dans un plan de part et d'autre de la verticale. Le pendule ne peut aller à une hauteur supérieure à celle où il a commencé. De plus, plus le fil est long moins sa vitesse d'oscillation est élevée.
Lancé de balles
Deux balles identiques sont lachées en même temps. L'une d'entre elles est projetée verticalement (balle n°1) l'autre horizontalement (balle n°2). La résistance de l'air est négligeable.

Les deux balles atteignent la position la plus basse au même moment même si l'une des balles a été projetée horizontalement. Les deux balles avaient une vitesse initiale nulle et ont effectuée une chute libre.

Une balle est lancée verticalement. Sa vitesse décroît jusqu'à atteindre une vitesse nulle. La balle change alors de trajectoire et se dirige vers le sol. Sa vitesse augmente et est maximale au moment de l'impact avec le sol.
Un levier est une barre qui pivote autour d'un point fixe et qui est utilisée pour soulever ou déplacer des charges lourdes. Les objets utilisant le principe de levier sont nombreux, par exemple : une balance, des ciseaux, une brouette, un casse-noisette, un coupe ongles, une agrafeuse, un pied de biche, une pince à épiler, un ouvre bouteille, un arrache clou ...
Loi de levier
Une bascule est équilibrée lorsque deux masses identiques sont placées à une même distance du pivot.

Une bascule est équilibrée lorsque pour deux objets le produit de leur masse par leur distance du pivot est égal.

Loi de levier : M1 x d1 = M2 x d2
Ce qui se vérifie facilement : M1 = 2 M2 et d2 = 2 d1.
Ainsi, deux corps s'équilibrent à des distances inversement proportionnelles à leur poids.
Les 3 genres de levier
Il existe 3 genres de leviers en fonction de la position des points d'appui, d'action et d'effet.
Premier genre

Ex: ciseaux, pince plate, balancoire, arrache clou
Deuxième genre

Ex: décapsuleur, brouette, agrafeuse, casse noix
Troisième genre

Ex: bat de baseball, pince à épiller, pince à sucre, canne à pêche, coupe ongle
La plupart des questions concerne les leviers du premier genre.
Pour réussir ce genre de test, il faut retenir que :
- plus la charge à soulever est proche du point d'appui, plus il est facile de la déplacer,
- plus le levier est long, plus c'est facile de déplacer la masse.
Cas particulier

avec M1 = 1, M2 = 2, M3 = 3, d1 = 5, d2 = 3, d3 = 2, d4 = 5
M1.d1 + M2.d2 = M3.d3 + M4.d4
1 x 5 + 2 x 3 = 3 x 2 + 5 x M4
M4 = 1
Les roues dentées sont fréquement utilisées dans les tests mécaniques. Elles sont associées pour former un engrenage qui permet de transmettre un mouvement de rotation. Les roues sont fixées à un arbre rotatif entrainé par une source d'énergie.
Rotation inverse
Les roues dentées en contact l'une de l'autre (exemple: mécanisme horlogé) tournent dans des sens opposés.

Rotation dans le même sens
Les roues dentées reliées par une chaine (exemple: vélo) tournent dans le même sens.

Vitesse de rotation
Lorsque les engrenages sont de la même taille et ont le même nombre de dents alors les roues tournent à la même vitesse.

Dans le cas où le nombre de dents est différent entre les roues, il faut alors faire le ratio du nombre de dents pour déterminer la vitesse d'une roue par rapport à l'autre.
Exemple :

Si la roue A fait 6 tours, combien de tours font les roues B et C?
Réponse :
Pour la roue B
Nombre de tours de B = Nombre de tours de A x Nombre de dents de A / Nombre de dents de B
soit Nombre de tours de B = 6 x 4 / 8 = 3
Pour la roue C
Nombre de tours de C = Nombre de tours de A x Nombre de dents de A / Nombre de dents de C
soit Nombre de tours de C = 6 x 4 / 6 = 4
Autre calcul équivalent :
Nombre de tours de C = Nombre de tours de B x Nombre de dents de B / Nombre de dents de C
soit Nombre de tours de C = 3 x 8 / 6 = 4
Une poulie est une roue associée à une chaîne, à une corde ou encore à un cable. Elle permet de soulever plus facilement une masse importante.
Poulie simple

La poulie simple permet d'exercer une force dans une direction différente sans en diminuer l'effort.
Poulie double

En associant 2 poulies, la force motrice est divisée par 2 alors que la distance de corde à tirer est multipliée par 2.
Ainsi, l'association de poulies, appelée communément palan, multiplie la force exercée par le nombre de poulies utilisées.
Sens de rotation

Dans le cas où la courroie est droite, les deux poulies tournent dans le même sens.

Dans le cas où la courroie est croisée, les deux poulies tournent en sens contraire.
Vitesse de rotation
Lorsque les roues sont de la même taille alors les roues tournent à la même vitesse. Par contre, lorsque leurs tailles sont différentes alors il faut faire le ratio de leur taille pour déterminer la vitesse d'une roue par rapport à l'autre.
Exemple :

Si la roue A fait 2 tours, combien de tours fait la roue B?
Note : Taille de A = 2 x Taille de B
Réponse :
Nombre de tour de B = Nombre de tour de A x Taille de A / Taille de B soit Nombre de tour de B = 2 x 2 / 1 = 4
Un treuil est un mécanisme qui permet d'enrouler un cable afin de porter ou tracter une charge. L'exemple le plus connu est le système de levage du seau dans un puit.

A l'aide de la manivelle, le treuil permet de soulever plus facilement la masse en utilisant le principe de levier. En effet, le bras de la manivelle est plus grand que le rayon du cylindre, ainsi l'effort pour soulever la masse est diminué. Ainsi plus la longueur de la manivelle est grande (ou plus le diamètre du cylindre est petit), moins l'effort à fournir est grand. Dans l'exemple, la force motrice pour soulever une même masse sera plus faible dans le cas 1.

Un plan incliné est une surface plane et inclinée qui permet de déplacer un objet entre deux niveaux. Pour mainternir le solide en équilibre, il faut appliquer une tension à l'aide d'un câble par exemple qui s'oppose au poids du solide et à l'action du plan incliné.
Inclinaison

Plus le plan est incliné, plus la force à fournir pour faire monter l'objet est importante.

Plus le plan est incliné, plus une bille lancée en haut du plan aura une vitesse élevée.
Dans le cas 2, la bille aura donc une vitesse supérieure à celle du cas 1 (pour un plan incliné de même longueur).
Frottement

Moins l'objet aura de frottement avec le plan incliné, plus celui-ci aura une vitesse élevée.
Dans le cas 1, la bille aura moins de frottement avec le plan incliné que dans le cas 2 donc une vitesse supérieure à celle du cas 2.
Equilibre

Cas 1 : les plans ont la même inclinaison, les billes sont identiques pour maintenir l'équilibre.
Cas 2 : l'un des plans est deux fois plus grand que l'autre, il faut deux billes pour maintenir l'équilibre.
Un ressort est un dispositif mécanique élastique qui retourne à sa forme initiale après avoir été comprimé ou étiré. Il se caractérise par sa raideur, noté k. La force exercée sur le ressort est liée à la raideur du ressort et à la longueur x d'allongement ou de compression : F = k . x
Montage en série

Dans le cas d'un montage en série, la raideur équivalente "K" d'un groupement de ressort se calcule à l'aide de la formule suivante : K = 1 / (1/k1 + 1/k2)
Montage en parallèle

Dans le cas d'un montage en parallèle, la raideur équivalente "K" d'un groupement de ressort se calcule à l'aide de la formule suivante : K = k1 + k2
Exemple type

Une masse d'un kilogramme est accrochée à deux ressorts en série qui sont étirés de 10 cm. Déterminer la distance d'étirement si les ressorts étaient en parallèle.
Réponse :
Une masse d'1 kg étire les deux ressorts en série de 10 cm; donc chaque ressort est étiré de 5 cm pour une charge de 1 kg. Le calcul de k dans le premier cas donne k = F1/x1 = 1/5 * g = 0.2 kg/cm * g avec F1 = masse * g, g est la constante de gravitation.
En parallèle chaque ressort subit donc un poids de 0.5 kg (la charge de 1 kg est répartie sur les deux ressorts donc 0.5 kg par ressort). La calcul de la déformation dans le second cas donne x2 = F2/k = 0.5/0.2 = 2.5cm (les constantes de gravitation s'annulent).
Déplacement
Déplacement en diagonale

Déplacement vertical (haut en bas ou inversement)

Déplacement horizontal (gauche à droite ou inversement)

Rotation
Rotation de 45° dans le sens horaire

Rotation de 90° dans le sens horaire

Rotation de 135° dans le sens horaire

Rotation de 180°

Rotation de 135° dans le sens anti-horaire

Rotation de 90° dans le sens anti-horaire

Rotation de 45° dans le sens anti-horaire

Symétrie
Symétrie axe vertical

Symétrie axe horizontal

Changement de couleur

Changement de forme

Multiplication du nombre d'éléments

Cube
Le test des cubes est un exercice de représentation dans l'espace. Il teste les capacités spatiales d'un individu à identifier, par exemple, la face opposée d'un cube, le cube obtenu à partir d'un cube à plat, ou encore le nombre de cubes d'une structure.Géométrie du cube
Les principales priorités d'un cube à connaître pour réussir les tests de cube sont listées ci-dessous.
Un cube à 6 faces

Seulement 3 faces sont visibles en même temps

Règle 1 : Deux faces opposées ne peuvent pas être adjacentes les unes aux autres
Les faces visibles ne peuvent jamais être en opposition l'une de l'autre.
Exemple :
Quelle lettre est à l'opposé de la lettre A?
 Réponse : la lettre C. En sachant que les 3 faces visibles ne peuvent pas être opposées, les figures 1 et 2 nous permettent d'éliminer les lettres B, D et E. La figure 3 nous confirme que la lettre opposée à A est C.
Réponse : la lettre C. En sachant que les 3 faces visibles ne peuvent pas être opposées, les figures 1 et 2 nous permettent d'éliminer les lettres B, D et E. La figure 3 nous confirme que la lettre opposée à A est C.Règle 2 : Si pour 2 dés, 2 faces sont adjacentes et l'une des 2 faces est à la même position, alors les 2 autres faces visibles sont opposées
Exemple :
Quelle lettre est à l'opposé de la lettre B?
 Réponse : la lettre D. Les lettres A et E sont adjacentes sur les deux cubes et E est à la même position, ainsi les deux autres lettres sont forcément opposées.
Réponse : la lettre D. Les lettres A et E sont adjacentes sur les deux cubes et E est à la même position, ainsi les deux autres lettres sont forcément opposées.Règle 3 : Si sur 2 dés une seule face est commune et à la même position, alors les faces opposées ont la même position
Exemple :
Quelle lettre est à l'opposé de la lettre B?
 Réponse : la lettre D. La lettre A est commune et à la même position sur les 2 dés, ainsi la lettre B est opposée à la lettre D (et C à E).
Réponse : la lettre D. La lettre A est commune et à la même position sur les 2 dés, ainsi la lettre B est opposée à la lettre D (et C à E).Il existe 11 patrons du cube




L'analyse du patron permet de trouver rapidement le cube qui en résulte.
Exemple 1 :

Sur ce patron, nous avons 1 opposé à 6, 2 à 5, 3 à 4.
Exemple 2 :
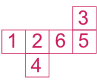
Sur ce patron, nous avons 1 opposé à 6, 2 à 5, 3 à 4.
Exemple 3 :
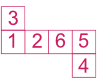
Sur ce patron, nous avons 1 opposé à 6, 2 à 5, 3 à 4.
Exemple 4 :
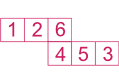
Sur ce patron, nous avons 1 opposé à 6, 2 à 5, 3 à 4.
Cas particulier : le dé
L'addition du nombre de points (ou chiffres) des faces opposées d'un dé standard est toujours égale à 7. De plus, la somme de deux faces adjacentes ne peut pas être égale à 7.
Exemple :
Quelle chiffre est à l'opposé du 1?
 Réponse : le chiffre 6.
Réponse : le chiffre 6.Nous constatons que la somme de deux faces adjacentes n'est jamais égale à 7.
Structure : découpe d'un cube

Si nous découpons ce cube en X parts (ici X = 3), nous obtenons différents types de cubes :
Cubes centraux :
1 seule face visible (représentée par une croix).
Nombre de cubes centraux = 6 (X-2)2 = 6 (3-2)2 = 6
Cubes au milieu :
2 faces visibles (représentées en blanc).
Nombre de cubes au milieu = 12 (X-2) = 12 (3-2) = 12
Cubes au coin :
3 faces visibles (représentées en couleur).
Nombre de cubes au coin = 8 (toujours égal à 8)
Cubes au centre :
0 face visible.
Nombre de cubes au centre = (X-2)3 = 1
Le nombre total de cubes est obtenu par la formule: X3 = 27
Structure : empilement de cubes
Les figures ci-dessous montrent l'empilement de cubes sur plusieurs étages :

Pour 1 étage, nous avons 1 cube, pour 2 étages 4 cubes, pour 3 étages 10 cubes.
Pour les compter facilement, nous vous conseillons de le faire par colonne en plaçant votre regard de côté. Par exemple, pour la dernière figure, nous obtenons 6 + 3 + 1 = 10.
Un autre exemple d'empilement :

Pour 1 étage, nous avons 1 cube, pour 2 étages 5 cubes, pour 3 étages 14 cubes.
Pour les compter facilement, nous vous conseillons de le faire par ligne en plaçant votre regard de face. Par exemple, pour la dernière figure, nous obtenons 1 + 4 + 9 = 14.
Structure : nombre de faces
Dans certains exercices, vous devrez compter le nombre de faces d'une structure.
Exemple :
 Réponses : 12 et 9.
Réponses : 12 et 9.Test de logique codes
Test des opérateurs
Dans le test des opérateurs, une forme est désignée par une lettre. Si celle-ci est accompagnée d'un sigle, elle subit une transformation qu'il faut identifier (changement de couleur, de taille, de position ...).
Exemple :

Le sigle o indique que la forme subit une rotation de 90° dans le sens horaire.
Exemple de question:


 Le sigle Δ indique que la forme subit une rotation de 45° dans le sens anti-horaire; la bonne réponse est la n°1.
Le sigle Δ indique que la forme subit une rotation de 45° dans le sens anti-horaire; la bonne réponse est la n°1.Test des opérations codées
Le test des opérations codées consiste à résoudre un système d'équations à partir de symboles.
Exemple : ◍ = ▢ + 2 ◍ = ▢ + ▢ Il est plus facile de résoudre le système en remplaçant les symboles par des lettres. x = y + 2 x = y + y = 2 y Méthode par substitution : une inconnue est exprimée en fonction de l'autre puis elle est remplacée dans la seconde équation. x = 2 y = y + 2 y = 2 et x = 4 y = 2 Ainsi : ◍ = 4 et ▢ = 2
Test des tableaux codés
Le but des tests des tableaux codés est de retrouver la valeur de symboles regroupés dans une grille à partir d'opérations fournies afin de résoudre une nouvelle opération.
Les règles logiques sont nombreuses, il convient d'observer l'agencement des symboles et d'y retrouver par exemple une symétrie, une progression horizontale ou verticale, une opération en ligne ou en colonne ...
Exemple :

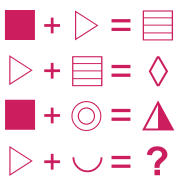 Réponse :
Réponse : 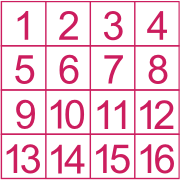
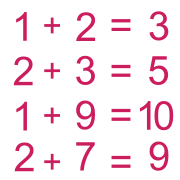
Test de substitution
Dans le test de substitution, les lettres d'un mot ou d'une phrase sont remplacées par exemple par des chiffres. Il faut retrouver le code de substitution afin de déterminer le mot ou la phrase qui correspond au codage.
Exemple : Quel est le mot codé? 1 18 2 18 5 Réponse : Le mot est A R B R E, les chiffres correspondent au rang des lettres dans l'alphabet.
Pour commencer ce genre de test, il est important de se noter l'alphabet numéroté en ordre croissant et décroissant. En effet, de nombreuses questions utilisent le rang des lettres dans l'alphabet.
A
B
C
D
E
F
G
H
I
J
1
26
2
25
3
24
4
23
5
22
6
21
7
20
8
19
9
18
10
17
K
L
M
N
O
P
Q
R
S
T
11
16
12
15
13
14
14
13
15
12
16
11
17
10
18
9
19
8
20
7
U
V
W
X
Y
Z
21
6
22
5
23
4
24
3
25
2
26
1
A partir du tableau, il devient facile de remplacer les lettres par leur numéro d'ordre et de retrouver la logique de progression.
Type 1 - Test de substitution avec indice
Exemple 1 : Si B S C S F correspond à A R B R E alors à quoi correspond T B Q J O?
Réponse : S A P I N, chaque lettre est remplacée par celle qui la succède dans l'ordre alphabétique.
Exemple 2 : Si 1 18 2 18 5 correspond à A R B R E alors à quoi correspond 19 1 16 9 14?
Réponse : S A P I N, chaque lettre est remplacée par son rang dans l'alphabet.
Type 2 - Test de substitution sans indice
Ce type de test de substitution est plus difficile car il fait appel à votre sens de la perspicacité.
Pour trouver la logique de codage, vous devez commencer par repérer les lettres isolées qui sont A ou Y, les apostrophes qui sont toujours suivies d'une voyelle, les lettres les plus fréquentes dans la langue française : E, S, A, I, T et enfin les petits mots qui sont souvent des articles (le, la, de, ...).
Exemple : 18 - 7 - 22 - 11 - 22 3 18 - 7 - 22 - 11 - 22 14 ' 17 - 11 - 21 - 7 - 3 - 23 8 - 3 - 11 - 22 21 - 17 - 16 16 - 11 - 6 Réponse : le chiffre 3 correspond à une lettre isolée et est donc forcément A ou Y. Comme le chiffre est répété dans plusieurs mots, nous supposons que 3 = A.
Le chiffre 17 est derrière une apostrophe, ainsi il correspond à une voyelle. Entre 17 et 3, il y a 14 rangs qui les séparent; ainsi à partir de l'alphabet nous en déduisons que 17 = O.
Ainsi, nous trouvons la logique de codage : le chiffre correspond au rang de la lettre dans l'alphabet + 2.
PETIT A PETIT L ' OISEAU FAIT SON NID
Test d'orientation dans l'espace
Les tests d'orientation évaluent vos capacités à vous déplacer dans l'espace.
Les ordres peuvent être donnés de plusieux façons :
- à l'aide des points cardinaux Nord - Est - Sud - Ouest (par exemple : direction Sud-Est)

- par des directions en degrés

- par des changements de cap exprimés en heure (par exemple : cap à 3 heure, soit un changement de direction de 90° dans le sens horaire par rapport à la direction initiale).

Test de la boussole type pilote
Le test de la boussole nécessite de suivre des instructions afin de trouver une direction finale.
Exemple 1 : Question 1 : Un coureur oriente sa boussole au nord et se dirige comme indiqué ci-dessous. Quelle est sa direction?
 Réponse 1 : Il suffit de compléter les points cardinaux pour connaître la direction du coureur :
Réponse 1 : Il suffit de compléter les points cardinaux pour connaître la direction du coureur :  Il se dirige vers l'ouest. Question 2 : Puis, il suit les changements de direction suivants : cap à 3 heures puis cap à 6 heures. Quelle est sa direction finale? Réponse 2 : Cap à 3 heures : il pivote de 90° dans le sens horaire par rapport à sa position initiale, il se dirige maintenant vers le nord.
Il se dirige vers l'ouest. Question 2 : Puis, il suit les changements de direction suivants : cap à 3 heures puis cap à 6 heures. Quelle est sa direction finale? Réponse 2 : Cap à 3 heures : il pivote de 90° dans le sens horaire par rapport à sa position initiale, il se dirige maintenant vers le nord.  Cap à 6 heures : il pivote de 180°, il fait un demi tour, il se dirige maintenant vers le sud.
Cap à 6 heures : il pivote de 180°, il fait un demi tour, il se dirige maintenant vers le sud.  Il se dirige donc vers le sud.
Il se dirige donc vers le sud.Exemple 2 : Question 1 : Un nageur oriente sa boussole au nord et se dirige comme indiqué ci-dessous. Après 5 minutes de nage, cap au nord. Puis, après 10 minutes, cap à 6 heures. Puis, après 5 minutes, cap à 3 heures pendant 5 minutes. Combien de temps le nageur se dirige-t-il vers le nord?
 Réponse : Le nageur commence par 5 minutes vers l'est.
Réponse : Le nageur commence par 5 minutes vers l'est.  Puis il se dirige au nord pendant 10 minutes.
Puis il se dirige au nord pendant 10 minutes.  Puis cap à 6 heures, ce qu'il signifie qu'il fait demi-tour, il se dirige donc au sud pendant 5 minutes.
Puis cap à 6 heures, ce qu'il signifie qu'il fait demi-tour, il se dirige donc au sud pendant 5 minutes.  Puis cap à 3 heures, ce qu'il signifie qu'il fait 90° dans le sens horaire par rapport à sa direction actuelle, il se dirige donc à l'ouest pendant 5 minutes.
Puis cap à 3 heures, ce qu'il signifie qu'il fait 90° dans le sens horaire par rapport à sa direction actuelle, il se dirige donc à l'ouest pendant 5 minutes.  Le nageur se dirige donc 10 minutes vers le nord
Le nageur se dirige donc 10 minutes vers le nordTest de déplacement dans une grille
Le test de déplacement dans une grille nécessite de suivre des instructions afin de trouver la case finale.
Exemple : Il faut se déplacer dans la grille en suivant les instructions suivantes : 2N-3O-1SE.

 Réponse : L'instruction 2N-3O-1SE, signifie qu'il faut aller 2 cases vers le nord puis 3 cases vers l'ouest et enfin 1 case vers le sud-est. Grâce à la boussole, nous déduisons les directions à prendre.
Réponse : L'instruction 2N-3O-1SE, signifie qu'il faut aller 2 cases vers le nord puis 3 cases vers l'ouest et enfin 1 case vers le sud-est. Grâce à la boussole, nous déduisons les directions à prendre. 

La case finale est C5.
Test de pliage
Test de pliage combiné
Le but des tests de pliage combiné est de trouver la figure qui est formée lorsqu'une feuille transparente avec des dessins sur chaque côté d'une ligne en pointillé est pliée le long de cette ligne.
Exemple :
Réponse : 1 Au final, cela revient à faire la symétrie de la moitié de la feuille par rapport à la ligne en pointillé.
Test de pliage découpé
Le but des tests de pliage découpé est de trouver la figure qui est formée lorsqu'une feuille pliée est découpée puis de nouveau dépliée.
Exemple :



 Réponse : 1
Réponse : 1Logique déductive - Position
Le test de logique déductive consiste à établir une conclusion à partir d'un ensemble d'hypothèses.
Ainsi, dans le test des positions logiques, il faut retrouver la position d'un objet à partir d'une série d'affirmations. La disposition des éléments peut être linéaire (exemple: aligné en rang) ou encore circulaire (exemple: assis autour d'une table).
Arrangement linéaire
Direction
- Lorsque la direction n'est pas mentionnée, il faut orienter la figure ainsi :

A est juste à gauche de B
A, B, C, D sont à gauche de E
C est juste à droite de B
C, D, E sont à droite de B
- Lorsque la direction est indiquée vers vous, il faut orienter la figure ainsi :

A est juste à droite de B
A, B, C, D sont à droite de E
C est juste à gauche de B
C, D, E sont à gauche de B
- Lorsqu'il y a deux lignes, les directions peuvent être différentes en fonction de la ligne:

A est juste à droite de B
A, B sont à droite de C
A est à l'opposé de D
A est diagonalement opposé à F
B est à l'opposé de E
D est juste à gauche de E
D, E sont à gauche de F
Règles
Règle 1

Si A est à côté de B, alors il y a 2 cas possibles :
- A est sur le côté gauche de B (cas 1)
- A est sur le côté droit de B (cas 2)
Règle 2

Si B est assis entre A et C, alors il y a 2 cas possibles :
- A est sur le côté gauche de B et C sur le côté droit de B (cas 1)
- A est sur le côté droit de B et C sur le côté gauche de B (cas 2)
Exemple Lisez attentivement ces informations :
- 5 élèves sont assis en ligne face au nord
- Marc est juste à gauche d'Anne
- Julie est entre Pierre et Sophie
- Sophie est entre Marc et Julie
Qui est au centre? Réponse D'après l'énoncé, nous savons :
- 5 élèves sont assis en ligne face au nord

- Marc est juste à gauche d'Anne

- Julie est entre Pierre et Sophie

- Sophie est entre Marc et Julie

A partir de ces éléments, nous pouvons déduire que Sophie est assise au milieu.

Arrangement circulaire
Le but est de retrouver la position d'éléments ou de personnes répartis de façon circulaire. Ils peuvent être disposés autour d'une table ronde ou rectangulaire ou de tout autre arrangement en boucle fermée.
Direction
- Les objets ou personnes peuvent être orientés face au centre :

A est juste à droite de B
A, D sont à droite de B
A est à l'opposé de C
C est juste à droite de D
- Les objets ou personnes peuvent être orientés dos au centre :

A est juste à gauche de B
A, B sont à droite de D
C est juste à droite de B
B est à l'opposé de D
Règles
Les règles sont les mêmes que celles des arrangements linéaires.
Exemple Lisez attentivement ces informations :
- 5 élèves sont assis face à face autour d'une table
- Marc est juste à gauche d'Anne
- Julie est entre Pierre et Sophie
- Sophie est entre Marc et Julie
Qui est à droite d'Anne? Réponse D'après l'énoncé, nous savons :
- 5 élèves sont assis en ligne face au nord

- Marc est juste à gauche d'Anne

- Julie est entre Pierre et Sophie

- Sophie est entre Marc et Julie

A partir de ces éléments, nous pouvons déduire que Pierre est assis à droite d'Anne.

Test des liens de parenté
Dans certaines questions de logique, il faudra identifier les liens de parenté qui existent entre plusieurs individus, c'est à dire la relation qui les lie entre eux.
Pour se préparer à ce type de test, il est indispensable de connaître certaines expressions que nous vous listons ci-dessous.
Degrés de parenté
Le fils du père (ou de la mère) Le frère La fille du père (ou de la mère) La soeur Le père du père (ou de la mère) Le grand père La mère du père (ou de la mère) La grand-mère L'épouse du fils (ou de la fille) La belle-fille ou la bru L'époux de la fille (ou du fils) Le beau-fils ou le gendre Le père de l'époux (ou de l'épouse) Le beau-père La mère de l'époux (ou de l'épouse) La belle-mère Le frère de l'époux (ou de l'épouse) Le beau-frère La soeur de l'époux (ou de l'épouse) La belle-soeur L'époux de la soeur (ou du frère) Le beau-frère L'épouse du frère (ou de la soeur) La belle-soeur Le fils du frère (ou de la soeur) Le neveu La fille du frère (ou de la soeur) La nièce Le frère du père (ou de la mère) L'oncle La soeur du père (ou de la mère) La tante L'épouse de l'oncle La tante L'époux de la tante L'oncle L'enfant de l'oncle (ou de la tante) Le cousin
Lien de parenté simple
Lien de parenté direct
Dans ce type d'exercice, il faut retrouver la relation qui lie deux personnes directement.
Pour cela, il faut décomposer la phrase en partant de la fin de l'énoncé et en remontant jusqu'au verbe.
Exemple :
En montrant Marc, Sophie dit : "il est le fils de la fille unique du mari de ma mère".
Quel est le lien entre Marc et Sophie?
Solution :
En partant de la fin de la phrase:
- le mari de ma mère = son père (hypothèse)
- la fille unique de son père = elle-même (Sophie)
- le fils de Sophie = son fils
Marc est le fils de Sophie A noter que nous sommes obligés de supposer que le "mari de sa mère" soit son père. Pour valider l'hypothèse, il faut écarter les autres réponses proposées.
Exemple :
En discutant de Faustine, Florian dit : "elle est l'unique fille de la mère de mon frère".
Quel est le lien entre Faustine et Florian?
Solution :
En partant de la fin de la phrase:
- la mère de mon frère = ma mère
- l'unique fille de ma mère = ma soeur
Faustine est la soeur de Florian
Lien de parenté indirect
Dans ce type d'exercice, il faut retrouver la relation qui lie deux personnes indirectement.
Pour cela, il faut décomposer la phrase en deux parties; tout d'abord en partant de la fin de l'énoncé et en remontant jusqu'au verbe et ensuite en partant du sujet de la phrase jusqu'au verbe.
Exemple :
En montrant Antoine, Marie dit : "la mère de sa soeur est la fille unique de ma grand-mère".
Quel est le lien entre Antoine et Marie?
Solution :
En partant de la fin de la phrase:
- la fille unique de ma grand-mère = la mère de Marie
En partant du début de la phrase:
- la mère de sa soeur = la mère d'Antoine
Ainsi, la mère d'Antoine est la mère de Marie, donc Antoine est le frère de Marie.
Exemple :
En introduisant Pierre, Lucie dit : "la seule fille de sa mère est ma mère".
Quel est le lien entre Pierre et Lucie?
Solution :
En partant de la fin de la phrase:
- ma mère = la mère de Lucie
En partant du début de la phrase:
- la seule fille de sa mère = la soeur de Pierre
Ainsi, la soeur de Pierre est la mère de Lucie, donc Pierre est l'oncle de Lucie
Lien de parenté commun
Dans ce type d'exercice, il faut retrouver les relations qui lient plusieurs personnes.
Pour cela, il faut décomposer la phrase en essayant par exemple de créer un arbre généalogique.
Exemple :
A et B sont soeurs. C et D sont frères. La fille de A est la soeur de D.
Quel est le lien entre B et C? Solution : La fille de A est la soeur de D donc A est la mère de C et D ainsi B, qui est la soeur de A, est la tante de C.
Exemple :
A et B sont mariés. C et D sont frères. A est la soeur de C.
Quel est le lien entre B et D? Solution : A est la soeur de C donc A, C et D sont frères et soeur ainsi B, qui est le mari de A, est le beau-frère de D.
Lien de parenté codé
Dans ce type d'exercice, les relations qui lient plusieurs personnes sont codées par des symboles comme + - x / etc..
Exemple :
On sait que : A + B signifie que A est la soeur de B A - B signifie que A est le frère de B A x B signifie que A est la fille de B
Quelle est l'équation qui montre que C est l'oncle maternel de D? a) E - C + D b) D + E - C c) D x E + C d) E x D + C
Solution : Réponse c) C est l'oncle maternel de D
donc C est le frère de la mère de D
ou D est la fille de la soeur de C
ainsi si la mère = E, nous avons D x E + C
Nous pouvons vérifier facilement cette réponse : D x E + C = D "est la fille de" E "qui est la soeur de" C
Pour les autres propositions a) E - C + D : E "est le frère de" C "qui est la soeur de" D soit C est la soeur de D b) D + E - C : D "est la soeur de" E "qui est le frère de" C soit C est la soeur (ou le frère?) de D d) E x D + C : E "est la fille de" D "qui est la soeur de" C soit C est la tante de ETEST MATHEMATIQUE
- Rotation et symétrie
- Carre logique
- Case a noircir
- Matrice
- Série lettres
- Série numérique
- Série alpha numérique
- Logique numerique
- Intrus nombre
- Intrus lettre
- Serie graphique
- Intrus graphique
- Analogie visuel
- Cube
- Orientation
- Codes
- Pliage
- Position
- Lien de parenté
- Jeu du Simon
- Jeu du mémoire
- Jeu de l'image
- Jeu du denombrement
- Jeu de la commande
- Jeu des couleurs
- Jeu des nombres
- Jeu des lettres
- Jeu des caisses noires
TEST MECANIQUE
Les tests de raisonnement mécanique sont conçus pour évaluer vos connaissances techniques, mécaniques et physiques. Ils contiennent généralement des questions qui ne nécessitent pas de connaissances particulières, mais qui font appel à votre sens physique.
Les notions physiques régulièrement présentent dans ce genre de tests sont l'électricité, la mécanique (par exemple les balances, les leviers, les engrenages, les manivelles et les poulies), les structures (par exemple les effets de la compression), l'énergie (par exemple la transmission de la chaleur, la lumière et la puissance), les forces (par exemple la pesanteur, les effets de rotation, comme la force centrifuge).
Electricité
Un circuit électrique comprend : une source électrique (exemple: batterie, prise électrique), du fil électrique, un appareil électrique et un interrupteur (option) pour controler le circuit.

Symboles
Interrupteur :

Ampoule :

Batterie :

Prise :

Deux fils connectés :

Deux fils non connectés :

Fusible :

Pour fonctionner, un circuit a besoin d'être fermé, c'est à dire que toutes les parties du circuit doivent être connectées.
Exemple :

L'interrupteur est ouvert, le circuit n'est pas fermé, la lampe ne s'allume pas.

L'interrupteur est fermé, le circuit est fermé, la lampe s'allume.
Circuit en série - parallèle

La lampe 1 est en série alors que les lampes 2 et 3 sont installées en parallèle.
Si la lampe 1 est supprimée, le circuit est ouvert, toutes les lampes s'éteignent.
Si la lampe 2 est supprimée (ou la lampe 3), le circuit reste fermé, les autres lampes restent allumées.
Court circuit

L'interrupteur crée un chemin préférentiel pour l'électricité car il y a moins de résistance que le chemin avec l'ampoule. Ainsi, l'électricité passe par l'interrupteur et l'ampoule s'éteint quand l'interrupteur ferme le circuit.

Pour le cicuit 2, le cable supplémentaire court circuite le circuit, la lampe reste éteinte. Pour le circuit 1, le cable supplémentaire n'a pas d'incidence, la lampe reste allumée.
Connexion de batteries
Série

La lampe s'allume.

La lampe ne s'allume pas.
Parallèle

La lampe s'allume.
Gravité
La gravité est la loi physique qui explique l'attraction terrestre des corps. Cette force est verticale et dirigée vers le centre de la Terre.
Exemple :

Sachant que l'ensemble est à l'arrêt, la boule sera dirigée comme sur la figure 1. En effet, la gravité dirige la boule verticalement.
Vitesse et temps de chute d'un objet
La vitesse de chute d'un objet dans le vide ne dépend pas de son poids (en considérant que la force de résistance de l'air est négligeable). Ainsi, une bille en fer tombera à la même vitesse qu'une bille en plastique.
De plus, la durée de la chute est fonction uniquement de la hauteur de la chute et est indépendante de la masse.
Exemple :

Les deux balles tombent de la même hauteur, elles toucheront le sol en même temps.
Pendule

Le pendule doit son mouvement oscillatoire à l'effet de la pesanteur. Au bout d'un fil inextensible, une petite masse est accrochée. En écartant celle-ci de sa position d'équilibre, elle oscille dans un plan de part et d'autre de la verticale. Le pendule ne peut aller à une hauteur supérieure à celle où il a commencé. De plus, plus le fil est long moins sa vitesse d'oscillation est élevée.
Lancé de balles
Deux balles identiques sont lachées en même temps. L'une d'entre elles est projetée verticalement (balle n°1) l'autre horizontalement (balle n°2). La résistance de l'air est négligeable.

Les deux balles atteignent la position la plus basse au même moment même si l'une des balles a été projetée horizontalement. Les deux balles avaient une vitesse initiale nulle et ont effectuée une chute libre.

Une balle est lancée verticalement. Sa vitesse décroît jusqu'à atteindre une vitesse nulle. La balle change alors de trajectoire et se dirige vers le sol. Sa vitesse augmente et est maximale au moment de l'impact avec le sol.
Levier
Un levier est une barre qui pivote autour d'un point fixe et qui est utilisée pour soulever ou déplacer des charges lourdes. Les objets utilisant le principe de levier sont nombreux, par exemple : une balance, des ciseaux, une brouette, un casse-noisette, un coupe ongles, une agrafeuse, un pied de biche, une pince à épiler, un ouvre bouteille, un arrache clou ...
Loi de levier
Une bascule est équilibrée lorsque deux masses identiques sont placées à une même distance du pivot.

Une bascule est équilibrée lorsque pour deux objets le produit de leur masse par leur distance du pivot est égal.

Loi de levier : M1 x d1 = M2 x d2
Ce qui se vérifie facilement : M1 = 2 M2 et d2 = 2 d1.
Ainsi, deux corps s'équilibrent à des distances inversement proportionnelles à leur poids.
Les 3 genres de levier
Il existe 3 genres de leviers en fonction de la position des points d'appui, d'action et d'effet.
Premier genre

Ex: ciseaux, pince plate, balancoire, arrache clou
Deuxième genre

Ex: décapsuleur, brouette, agrafeuse, casse noix
Troisième genre

Ex: bat de baseball, pince à épiller, pince à sucre, canne à pêche, coupe ongle
La plupart des questions concerne les leviers du premier genre.
Pour réussir ce genre de test, il faut retenir que :
- plus la charge à soulever est proche du point d'appui, plus il est facile de la déplacer,
- plus le levier est long, plus c'est facile de déplacer la masse.
Cas particulier

avec M1 = 1, M2 = 2, M3 = 3, d1 = 5, d2 = 3, d3 = 2, d4 = 5
M1.d1 + M2.d2 = M3.d3 + M4.d4
1 x 5 + 2 x 3 = 3 x 2 + 5 x M4
M4 = 1
Roue dentée
Les roues dentées sont fréquement utilisées dans les tests mécaniques. Elles sont associées pour former un engrenage qui permet de transmettre un mouvement de rotation. Les roues sont fixées à un arbre rotatif entrainé par une source d'énergie.
Rotation inverse
Les roues dentées en contact l'une de l'autre (exemple: mécanisme horlogé) tournent dans des sens opposés.

Rotation dans le même sens
Les roues dentées reliées par une chaine (exemple: vélo) tournent dans le même sens.

Vitesse de rotation
Lorsque les engrenages sont de la même taille et ont le même nombre de dents alors les roues tournent à la même vitesse.

Dans le cas où le nombre de dents est différent entre les roues, il faut alors faire le ratio du nombre de dents pour déterminer la vitesse d'une roue par rapport à l'autre.
Exemple :

Si la roue A fait 6 tours, combien de tours font les roues B et C?
Réponse :
Pour la roue B
Nombre de tours de B = Nombre de tours de A x Nombre de dents de A / Nombre de dents de B
soit Nombre de tours de B = 6 x 4 / 8 = 3
Pour la roue C
Nombre de tours de C = Nombre de tours de A x Nombre de dents de A / Nombre de dents de C
soit Nombre de tours de C = 6 x 4 / 6 = 4
Autre calcul équivalent :
Nombre de tours de C = Nombre de tours de B x Nombre de dents de B / Nombre de dents de C
soit Nombre de tours de C = 3 x 8 / 6 = 4
Poulie
Une poulie est une roue associée à une chaîne, à une corde ou encore à un cable. Elle permet de soulever plus facilement une masse importante.
Poulie simple

La poulie simple permet d'exercer une force dans une direction différente sans en diminuer l'effort.
Poulie double

En associant 2 poulies, la force motrice est divisée par 2 alors que la distance de corde à tirer est multipliée par 2.
Ainsi, l'association de poulies, appelée communément palan, multiplie la force exercée par le nombre de poulies utilisées.
Sens de rotation

Dans le cas où la courroie est droite, les deux poulies tournent dans le même sens.

Dans le cas où la courroie est croisée, les deux poulies tournent en sens contraire.
Vitesse de rotation
Lorsque les roues sont de la même taille alors les roues tournent à la même vitesse. Par contre, lorsque leurs tailles sont différentes alors il faut faire le ratio de leur taille pour déterminer la vitesse d'une roue par rapport à l'autre.
Exemple :

Si la roue A fait 2 tours, combien de tours fait la roue B?
Note : Taille de A = 2 x Taille de B
Réponse :
Nombre de tour de B = Nombre de tour de A x Taille de A / Taille de B soit Nombre de tour de B = 2 x 2 / 1 = 4
Treuil
Un treuil est un mécanisme qui permet d'enrouler un cable afin de porter ou tracter une charge. L'exemple le plus connu est le système de levage du seau dans un puit.

A l'aide de la manivelle, le treuil permet de soulever plus facilement la masse en utilisant le principe de levier. En effet, le bras de la manivelle est plus grand que le rayon du cylindre, ainsi l'effort pour soulever la masse est diminué. Ainsi plus la longueur de la manivelle est grande (ou plus le diamètre du cylindre est petit), moins l'effort à fournir est grand. Dans l'exemple, la force motrice pour soulever une même masse sera plus faible dans le cas 1.
Plan incliné

Un plan incliné est une surface plane et inclinée qui permet de déplacer un objet entre deux niveaux. Pour mainternir le solide en équilibre, il faut appliquer une tension à l'aide d'un câble par exemple qui s'oppose au poids du solide et à l'action du plan incliné.
Inclinaison

Plus le plan est incliné, plus la force à fournir pour faire monter l'objet est importante.

Plus le plan est incliné, plus une bille lancée en haut du plan aura une vitesse élevée.
Dans le cas 2, la bille aura donc une vitesse supérieure à celle du cas 1 (pour un plan incliné de même longueur).
Frottement

Moins l'objet aura de frottement avec le plan incliné, plus celui-ci aura une vitesse élevée.
Dans le cas 1, la bille aura moins de frottement avec le plan incliné que dans le cas 2 donc une vitesse supérieure à celle du cas 2.
Equilibre

Cas 1 : les plans ont la même inclinaison, les billes sont identiques pour maintenir l'équilibre.
Cas 2 : l'un des plans est deux fois plus grand que l'autre, il faut deux billes pour maintenir l'équilibre.
Ressort
Un ressort est un dispositif mécanique élastique qui retourne à sa forme initiale après avoir été comprimé ou étiré. Il se caractérise par sa raideur, noté k. La force exercée sur le ressort est liée à la raideur du ressort et à la longueur x d'allongement ou de compression : F = k . x
Montage en série

Dans le cas d'un montage en série, la raideur équivalente "K" d'un groupement de ressort se calcule à l'aide de la formule suivante : K = 1 / (1/k1 + 1/k2)
Montage en parallèle

Dans le cas d'un montage en parallèle, la raideur équivalente "K" d'un groupement de ressort se calcule à l'aide de la formule suivante : K = k1 + k2
Exemple type

Une masse d'un kilogramme est accrochée à deux ressorts en série qui sont étirés de 10 cm. Déterminer la distance d'étirement si les ressorts étaient en parallèle.
Réponse :
Une masse d'1 kg étire les deux ressorts en série de 10 cm; donc chaque ressort est étiré de 5 cm pour une charge de 1 kg. Le calcul de k dans le premier cas donne k = F1/x1 = 1/5 * g = 0.2 kg/cm * g avec F1 = masse * g, g est la constante de gravitation.
En parallèle chaque ressort subit donc un poids de 0.5 kg (la charge de 1 kg est répartie sur les deux ressorts donc 0.5 kg par ressort). La calcul de la déformation dans le second cas donne x2 = F2/k = 0.5/0.2 = 2.5cm (les constantes de gravitation s'annulent).


PIX Lawnmower Belts offer solutions for each and every OEM application in every possible belt type and construction. PIX specializes in manufacturing, extensive range of Belts, exclusively designed to withstand the rigorous working conditions encountered in grass-machinery applications. Conforming to the highest quality standards, PIX-Lawn & Garden Belts are the perfect solution for all lawn & garden applications. PIX Garden / Lawn Mower Belts are expertly produced and developed using the highest standard technologies and materials to meet the toughest demands.It is thanks to the unrivaled reliability of these belts that PIX garden belts are one of the most respected brands in the lawn and garden belt industry.
RépondreSupprimercourroie de motoculture
YnietaeKriaru1982 Jay Blanco download
RépondreSupprimerstopcakerbbet