Test psychotechnique

 Test psychotechnique

Les tests psychotechniques comprennent : des tests verbaux, des tests de dominos, des tests de cartes, des tests mécaniques, des tests logique verbaux, des tests mathématiques et des tests de mémoire.

TEST VERBAL:

Les tests verbaux sont largement utilisés dans les tests de recrutement ou les tests de QI. Ils sont conçus pour mesurer la capacité verbale, c'est-à-dire la capacité à comprendre et à utiliser les mots.

• Vocabulaire مفردات اللغة

1. Synonyme
2. Antonyme
3. Homonyme
4. Paronyme

Synonyme - Homonyme - Antonyme - Paronyme

Test des synonymes

Les synonymes sont des mots qui ont le même sens ou un sens proche. Ainsi, lorsqu'un mot est remplacé par son synonyme dans une phrase, le sens de celle-ci ne doit pas être modifié.

Les synonymes appartiennent toujours à la même catégorie grammaticale: un verbe a pour synonyme un autre verbe, un nom un autre nom, un adjectif un autre adjectif ...

Exemple 1 : Quel est le mot qui a le sens le plus proche de PLAT?
1/ Plan - 2/ Inégal - 3/ Grand - 4/ Debout
Bonne réponse : Plan, par exemple "La surface est plate" ≈ "La surface est plane"
Le mot "PLAT" est utilisé comme adjectif.

Exemple 2 : Quel est le mot qui a le sens le plus proche de PLAT?
1/ Viande - 2/ Verre - 3/ Mets - 4/ Four
Bonne réponse : Mets, par exemple "Un plat appétissant" ≈ "Un mets appétissant"
Le mot "PLAT" est utilisé comme nom.

Ces exemples montrent que le synonyme à trouver n'a qu'un seul sens et n'appartient qu'à une seule classe grammaticale.

Test des antonymes

Les antonymes sont des mots qui ont des sens contraires ou éloigné.

Les antonymes appartiennent toujours à la même catégorie grammaticale: un verbe a pour antonyme un autre verbe, un nom un autre nom, un adjectif un autre adjectif ...

Exemple 1 : Quel est le mot qui a le sens le plus éloigné de PLAT?
1/ Plan - 2/ Inégal - 3/ Grand - 4/ Debout
Bonne réponse : Inégal, par exemple "La surface est plate" ≠ "La surface est inégale"
Le mot "PLAT" est utilisé comme adjectif.

Test des homonymes

Les homonymes sont des mots qui se prononcent de la même façon mais qui ont un sens différent.

Exemple 1 : Quel est le mot qui complète cette phrase : En quelques ......... de crayon, il avait fait son portrait.
1/ cous - 2/ coups - 3/ coûts
Bonne réponse : coups

Test des paronymes

Les paronymes sont des mots qui s'écrivent ou se prononcent presque de la même façon mais qui ont un sens différent.

Exemple 1 : Complétez cette phrase : Le début du spectacle est .....
1/ imminent - 2/ éminent
Bonne réponse : imminent
Imminent : qui va se produire dans un avenir proche.

Éminent : qui se distingue par sa notoriété (Mozart est un compositeur éminent).           

• Intrusدخيل

Ces exercices de français permettent de tester vos connaissances verbales et votre capacité à identifier rapidement un mot qui est différent des autres.

• Analogie verbalالتشبيه اللفظي

Ces exercices de français permettent de tester votre capacité à déterminer un mot à partir d'un cas parallèle.

• Proverbeمثل

Les tests de français de cette rubrique vous permettent de tester votre compréhension des phrases et plus particulièrement des proverbes et des expressions courantes.

• Orthographeهجاء

Les tests d'orthographe sont fréquemment utilisés lors des concours ou entretiens d'embauche afin d'évaluer les compétences du candidat. Les exercices de français ci-dessous sont basés sur les fautes d'orthographe les plus courantes.

• Genreنوع

Dans certains tests de français, vous devrez identifier le genre des noms, à savoir s'ils sont masculins ou féminins.

Liste des noms féminins difficiles

une acné	une acoustique	une aérogare
une alcôve	une amnistie	une anagramme
une antilope	une apostrophe	une apothéose
une appendicite	une arabesque	une arachide
une argile	une artère	une asperge
une atmosphère	une chrysalide	une ecchymose
une échappatoire	une éphéméride	une épice
une épithète	une idole	une idylle
une moustiquaire	une oasis	une octave
une omoplate	une orbite	une primevère
une réglisse	une stalactite	une stalagmite

Liste des noms masculins difficiles

un abaque	un accueil	un acouphène
un acrylique	un aéronef	un agrume
un ail	un amalgame	un ambre
un amiante	un anthracite	un antidote
un aphte	un apogée	un appendice
un armistice	un aromate	un arpège
un asphalte	un astérisque	un chrysanthème
un éclair	un éloge	un emblème
un en-tête	un entracte	un épiderme
un épilogue	un évangile	un exode
un globule	un haltère	un hémisphère
un hôpital	un horoscope	un hospice
un indice	un insigne	un interclasse
un intermède	un interstice	un ivoire
un obélisque	un opercule	un ovule
un pétale	un planisphère	un pore
un poulpe	un tentacule	un termite
un testicule	un tubercule	un viscère

• Anagrammeإعادة ترتيب الأحرف

Un anagramme est un mot formé en inversant ou permutant de place les lettres d'un autre mot.

Par exemple : Chien - Niche - Chine

Dans les tests psychotechniques, il est fréquent de retrouver les anagrammes car ils permettent d'analyser les facultés d'observation et d'attention du candidat mais aussi les connaissances en vocabulaire et en orthographe.

• Jeux de motsألعاب الكلمات

Dans ces exercices de français, il vous faudra retrouver des mots qui ont en commun soit des lettres soit un autre mot.

Lettres communes

1/ Il faut retrouver les lettres qui terminent le premier mot et qui commencent le second.

Exemple : MAI ... NERIE
Réponse : SON → maison & sonnerie

2/ Il faut retrouver les lettres communes qui complètent les mots.

Exemple : MAI... BI... SAI...
Réponse : SON → maison, bison & saison

Exemple : ...NERIE ...DE ...GER
Réponse : SON → sonnerie, sonde & songer

Mots communs

1/ Il faut retrouver le mot qui forme deux mots composés.

Exemple : CACHE ... COL
Réponse : CACHE → cache-cache & cache-col

2/ Il faut retrouver le mot commun qui complète les autres mots.

Exemple : ... BOUE ... CORPS ... MANGER
Réponse : GARDE → garde-boue, garde-corps & garde-manger

TEST DOMINOS

Parmi les tests psychotechniques les plus connus, on retrouve les tests de dominos. Nous vous proposons ici des tests incluant les principaux cas de figures que vous êtes susceptibles de rencontrer si vous êtes amenés à réaliser ce genre de test dans le cadre d'un entretien d'embauche, de concours administratifs (infirmière IFSI, gendarmerie, ...), à l'école, ....

Règle du test de dominos

Des dominos sont positionnés de manière linéaire ou suivant des dispositions plus complexes. Le but de l'exercice est d'analyser les dominos afin de trouver la règle de construction générale et ainsi pouvoir compléter le domino comportant des points d'interrogations ? à la place des points.

Avant de commencer il est important de rappeler qu'un domino est divisé en deux parties dont la valeur est comprise entre 0 et 6. Ainsi, une suite de dominos se compose de la façon suivante :

      

N'oubliez pas le 0 qui correspond à la case vide. Ainsi, dans une suite croissante, la valeur qui suit le 6 est le 0.

Position des dominos

Les dominos peuvent être disposés de différentes façons. Les représentations les plus courantes sont listées ci-dessous.

Présentation en ligne

    
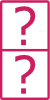Réponse :

Chaque moitié progresse de un point.

Présentation en double ligne

  
  
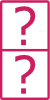Réponse :

Lecture horizontale : chaque moitié progresse de un point.

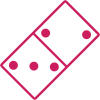
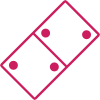
Présentation en rectangle

  
  
  
Réponse :

Lecture horizontale : chaque moitié progresse de un point.

Présentation en colonne

Réponse :

Chaque moitié progresse de un point.

Présentation en spirale

Réponse :

Chaque moitié progresse de un point (entre chaque moitié).

Présentation en croix

Réponse :

On a une symétrie centrale.

Présentation en cercle

Réponse :

Chaque moitié progresse de un point.

Principales règles logiques

Les exercices sont basés sur de nombreuses progressions dont les plus fréquentes sont reprises ici.

Progression positive - Suite croissante

   

Suite croissante de 2 en 2.
Attention n'oubliez pas le 0 dans la suite : 6 + 2 ≠ 2

Progression négative - Suite décroissante

   

Suite décroissante de 1 en 1.
Attention n'oubliez pas le 0 dans la suite : 1 - 1 ≠ 6

Progression combinée

    

Moitié supérieure : suite croissante de 1 en 1. Moitié inférieure : suite croissante de 2 en 2.

Progression croisée - Lecture en diagonale

   

Lecture en diagonale avec série croissante de 2 en 2 : 2 - 4 - 6 - 1 et 5 - 0 - 2 - 4

Progression cumulative - Opérations de base

Addition et Soustraction verticales

  
  
  

Exemple sur la première colonne :
Moitié supérieure du domino : 2 + 0 = 2
Moitié inférieure du domino : 5 - 3 = 2

Addition horizontale

  
  

Exemple sur la première lignne :
Partie supérieure du domino : 0 + 2 = 2
Partie inférieure du domino : 2 + 4 = 6

Multiplication horizontale

  
  
  

Exemple sur la première ligne :
Moitié supérieure du domino : 1 x 3 = 3
Moitié inférieure du domino : 2 x 1 = 2

Symétrie centrale

     

Symétrie centrale.

Symétrie axiale

  
  
  

Symétrie axiale.

Superposition des dominos

  
  

Superposition des deux premières colonnes pour obtenir la troisième colonne.

Similarité

  
  
  

Trois dominos identiques et alignés différemment sur chaque ligne .

Erreurs fréquentes

Suite non respectée

Oublie du 0 dans la suite.

     
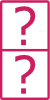Réponse :
 et non 
Suite croissante +1.

Somme des dominos

Somme des dominos pour obtenir le domino manquant.

   
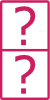Réponse :
 et non 
Suite croissante +1. 
Lorsque les dominos sont alignés sur une seule ligne, il faut retrouver une suite ou une symétrie par exemple, mais il ne faut pas se contenter d'additionner les dominos pour obtenir le domino manquant.

Logique incomplète

2 logiques à respecter pour obtenir le domino manquant.

Réponse :
 et non 
Suite décroissante de 1 en 1 : 5 (3) 4 (2) 3 (1) 
Chaque domino dont la somme des 2 cases est égale à 4 peut fonctionner mais cette logique n'est pas complète.
En effet, il faut observer une suite décroissante en lecture verticale (1ère colonne : 2-1-0 et 4-3-2; 3ème colonne : 5-4-3 et 3-2-1).

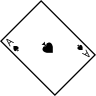
TEST CARTES

Les tests de cartes à jouer sont directement inspirés des tests de dominos. Ils sont souvent proposés lors d'entretien d'embauche, de concours administratifs ou encore lors de tests de sélection (école d'infirmiers, gendarmerie, ...).

Règle du test de cartes à jouer

Chaque question regroupe un nombre de cartes dont l'une d'entre elles est retournée. Il faut en déterminer à la fois le chiffre mais aussi la couleur en fonction de la position et des caractéristiques des autres cartes.

La valeur de la carte suit une progression arithmétique en boucle : as, 2, 3, 4, 5, 6, 7, 8, 9, 10, as, 2, 3 ..., avec l'as qui compte pour 1. Dans les tests officiels, les figures ne sont pas utilisées : valet, dame, roi. Il arrive que le joker soit présent mais il n'a pas de valeur, il doit être considéré comme une carte neutre.

Le deuxième paramètre est la couleur: coeur ♥, carreau ♦, pique ♠ ou trèfle ♣. Contrairement à certains jeux de cartes, il n'y a pas de supériorité entre les couleurs.

.

Position des cartes à jouer

Les cartes à jouer peuvent être disposés de différentes façons. Les représentations les plus courantes sont listées ci-dessous.

Présentation en ligne

Réponse :

Chaque carte progresse de un point.

Présentation en double ligne

Réponse :
 
Lecture horizontale : chaque carte progresse de un point.

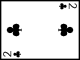
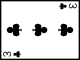
Présentation en rectangle

Réponse :

Lecture horizontale : chaque carte progresse de un point.

Présentation en colonne

Réponse :

Chaque carte progresse de un point.

Présentation en spirale

Réponse :

Chaque carte progresse de un point.

Présentation en croix

Réponse :

Chaque carte progresse de un point.

Présentation en cercle

Réponse :

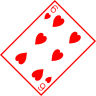
Chaque carte progresse de un point et alterne de couleur entre pique et coeur.

Principales règles logiques

Les exercices sont basés sur de nombreuses progressions dont les plus fréquentes sont reprises ici.

Progression positive - Suite croissante

Suite croissante de 1 en 1 avec une alternance des couleurs.

Progression négative - Suite décroissante

Suite décroissante de 1 en 1 avec une alternance des couleurs.

Progression croisée - Lecture en diagonale

Lecture en diagonale avec une série croissante de 2 en 2 : 1 - 3 - 5 - 7 et une décroissante de 2 en 2 : 10 - 8 - 6 - 4

Progression cumulative - Opérations de base

Addition verticale

Exemple sur la première colonne : addition des cartes des 2 premières lignes pour obtenir la troisième ligne : 2 + 3 = 5. Une couleur par colonne.

Addition horizontale

Exemple sur la première ligne : addition des trois premières cartes pour obtenir la dernière carte : 1 + 8 + 1 = 10. Une couleur par colonne.

Multiplication verticale

Multiplication par 2 de la première ligne pour obtenir la deuxième. Lecture diagonale pour la couleur.

Symétrie centrale

Symétrie centrale.

Symétrie axiale

Symétrie axiale.

Similarité

Trois cartes identiques et alignées différemment sur chaque ligne .

TEST LOGIQUE
Les tests de logique sont fréquemment utilisés dans les tests de sélection, les tests les plus répandus sont :

Rotation & Symétrie

La rotation et la symétrie sont les principales transformations utilisées dans les tests graphiques. Ainsi, nous vous proposons une fiche de cours ainsi que plusieurs tests afin de vous familiariser avec ce type d'exercices.

Rotation

Sens horaire

Lorsque la figure pivote (ou se déplace) dans le sens horaire, la rotation se fait dans le :

• sens des aiguilles d'une montre
• sens anti-trigonométrique
• sens négatif
• sens indirect

Sens anti-horaire

Lorsque la figure pivote (ou se déplace) dans le sens anti-horaire, la rotation se fait dans le :

• sens contraire des aiguilles d'une montre
• sens inverse des aiguilles d'une montre
• sens trigonométrique
• sens positif
• sens direct

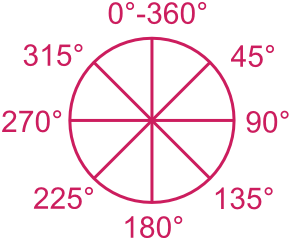
Angle de rotation

Rotation de 360° = Rotation de 0°
Rotation de 45° dans le sens horaire = Rotation de 315° dans le sens anti-horaire
Rotation de 90° dans le sens horaire = Rotation de 270° dans le sens anti-horaire
Rotation de 180° dans le sens horaire = Rotation de 180° dans le sens anti-horaire

Exemples de rotation

      

Symétrie

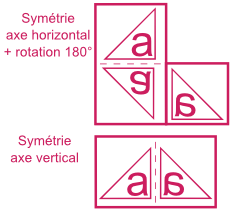
Symétrie sur l'axe vertical - Image dans un miroir

Dans une symétrie sur l'axe vertical, la figure pivote autour d'un axe de symétrie qui est vertical.

La figure obtenue est son image dans un miroir : les parties de gauche et de droite sont inversées mais pas les parties hautes et basses.

A noter que l'emplacement de l'axe de symétrie pour une symétrie sur l'axe vertical (à gauche ou à droite de la figure) conduit au même résultat.

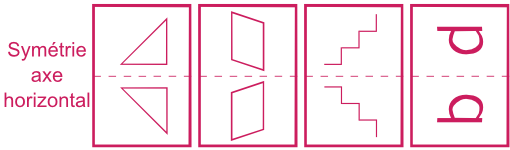
Symétrie sur l'axe horizontal - Reflet dans l'eau

Dans une symétrie sur l'axe horizontal, la figure pivote autour d'un axe de symétrie qui est horizontal.

La figure obtenue est son reflet dans l'eau : les parties hautes et basses sont inversées mais pas les parties de droites et de gauches.

A noter que l'emplacement de l'axe de symétrie pour une symétrie sur l'axe horizontal (en haut ou en bas de la figure) conduit au même résultat.

Symétrie des lettres et chiffres

Original	A	B	C	D	E	F	G	H	I	J
Axe vertical	A	B	C	D	E	F	G	H	I	J
Axe horizontal	A	B	C	D	E	F	G	H	I	J

Original	K	L	M	N	O	P	Q	R	S	T
Axe vertical	K	L	M	N	O	P	Q	R	S	T
Axe horizontal	K	L	M	N	O	P	Q	R	S	T

Original	U	V	W	X	Y	Z
Axe vertical	U	V	W	X	Y	Z
Axe horizontal	U	V	W	X	Y	Z

Original	a	b	c	d	e	f	g	h	i	j
Axe vertical	a	b	c	d	e	f	g	h	i	j
Axe horizontal	a	b	c	d	e	f	g	h	i	j

Original	k	l	m	n	o	p	q	r	s	t
Axe vertical	k	l	m	n	o	p	q	r	s	t
Axe horizontal	k	l	m	n	o	p	q	r	s	t

Original	u	v	w	x	y	z
Axe vertical	u	v	w	x	y	z
Axe horizontal	u	v	w	x	y	z

Original	0	1	2	3	4	5	6	7	8	9
Axe vertical	0	1	2	3	4	5	6	7	8	9
Axe horizontal	0	1	2	3	4	5	6	7	8	9

Combinaison de transformations

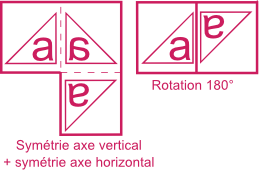
Symétrie sur l'axe vertical + symétrie sur l'axe horizontal

Une figure qui subit une symétrie sur l'axe vertical puis sur l'axe horizontal est identique à une figure qui subit une rotation de 180°.

Symétrie sur l'axe vertical + rotation 180°

Une figure qui subit une symétrie sur l'axe vertical puis une rotation de 180° est identique à une figure qui subit une symétrie sur l'axe horizontal.

Symétrie sur l'axe horizontal + rotation 180°

Une figure qui subit une symétrie sur l'axe horizontal puis une rotation de 180° est identique à une figure qui subit une symétrie sur l'axe vertical.

Carré logique - Mastermind

Les tests de carrés logiques, encore appelés tests Mastermind, ont pour support des lignes de chiffres, de lettres et plus rarement de figures géométriques. A partir des indications données pour chaque ligne, il faut déterminer la logique de l'exercice et ainsi trouver par déduction la solution recherchée, appelée "mot" (sans signification) ou encore "suite".

Codes

1 BP = un élément commun bien placé

2 BP = deux éléments communs bien placés

1 MP = un élément commun mal placé

2 MP = deux éléments communs mal placés

Exemple d'un carré logique - Mot de deux lettres

Trouver le "mot" de deux lettres, sachant que :

A	B	a une lettre commune bien placée - 1 BP
A	C	a une lettre commune mal placée - 1 MP

La réponse est : CB

A noter, que chaque élément n'apparaît qu'une seule fois dans un "mot". Il est ainsi impossible d'avoir commme solution AA, BB ...

1ère méthode - Raisonnement global

La lettre A ne peut pas être à la fois bien placée et à la fois mal placée en étant placée en position 1 sur les deux lignes. Ainsi, nous pouvons supprimer la lettre A du "mot" cherché.

La lettre B est donc forcément la lettre bien placée en deuxième position.

La lettre C est la lettre mal placée et doit être positionnée dans la première case.

Nous obtenons la réponse CB

2ème méthode - Raisonnement ligne par ligne

D'après la première ligne, nous savons que AB a une lettre commune avec le "mot" que nous cherchons et que celle-ci est bien placée.

Ainsi, la solution correspond à : A? ou ?B

D'après la deuxième ligne, nous savons que AC a une lettre commune avec le "mot" que nous cherchons et que celle-ci est mal placée.

Ainsi, la solution correspond à : ?A ou C?

Nous obtenons ainsi deux solutions possibles : AA ou CB

D'aprés les instructions, seule la solution CB est possible.

Exemple d'un carré logique - Mot de deux chiffres

Trouver le "mot" de deux chiffres, sachant que:

1	2	1 MP
2	3	1 MP

La réponse est : 31

Le raisonnement est le même que l'exemple précédent.

Nous avons : ?1 ou 2? et ?2 ou 3?

Ainsi la seule réponse possible est : 31

Exemple d'un carré logique - Mot de trois lettres

Trouver le "mot" de trois lettres, sachant que :

A	B	C	2 BP
A	C	D	1 BP
B	E	F	2 MP

La réponse est : ABE

1ère méthode - Raisonnement global

La lettre C ne peut pas être bien placée sur deux lignes à deux emplacements différents.

Ainsi, nous pouvons supprimer la lettre C du "mot" cherché; la solution est du type AB?

La lettre D est à éliminée car la lettre bien placée dans ACD est la lettre A.

La lettre F ne peut pas être présente en troisième position car aucune lettre dans BEFn'est bien positionnée. Ainsi, la troisième lettre est le E.

Nous obtenons la réponse ABE

2ème méthode - Raisonnement ligne par ligne

D'après la première ligne, nous savons que l'une de ces trois propositions est correcte : ?BC (cas 1) ou A?C (cas 2) ou AB? (cas 3).

Cas 1 :

?	B	C	2 BP
A	C	D	1 BP

La solution serait ABC, ce qui n'est pas possible car nous retrouvons la première ligne de l'énoncé qui ne comporte que 2 BP.

Cas 2 :

A	?	C	2 BP
A	C	D	1 BP

Nous avons deux lettres communes A et C entre les deux lignes, alors que dans la deuxième ligne il n'y a qu'une seule lettre commune possible (1BP). Ainsi cette solution n'est pas possible.

Cas 3 :

A	B	?	2 BP
A	C	D	1 BP
B	E	F	2 MP

Nous pouvons déduire de la deuxième ligne que les lettres C et D ne font pas parties du "mot" cherché.

La troisième ligne, nous confirme que la lettre B est commune avec notre "mot". De plus, nous pouvons déduire que la troisième lettre est la lettre E qui est également mal placée en deuxième position.

Nous obtenons bien la réponse ABE

Exemple d'un carré logique - Mot de trois chiffres

Trouver le "mot" de trois chiffres, sachant que :

1	2	3	1 BP
1	4	5	2 MP
4	1	3	1 MP

La réponse est : 524

1 et 3 ne peuvent être à la fois bien placés et mal placés donc sont à éliminer.

2 est bien placé en position 2; le chiffre est donc en deuxième position.

4 est mal placé en position 1 et 2; le chiffre est donc en troisième position.

5 est mal placé en position 3; le chiffre est donc en première position.

La réponse est bien : 524

Exemple d'un carré logique - Mot de quatre lettres

Trouver le "mot" de quatre lettres, sachant que :

A	B	C	D	2 BP
C	D	A	B	2 MP
E	F	C	D	2 MP
C	D	F	E	2 MP

La réponse est : ABEF

C et D ne peuvent être à la fois bien placées et mal placées donc sont à éliminer.

A et B sont bien placées en position 1 et 2.

E est mal placée en position 4; la lettre est donc en troisième position.

F est mal placée en position 3; la lettre est donc en quatrième position.

La réponse est bien : ABEF

Cases à noircir - Plateaux

Les tests de cases à noircir, encore appelés tests de plateaux ou logigrammes, consistent à noircir les cases d'un tableau quadrillé en fonction des instructions données en début de ligne et de colonne.

Exemple:

	2	3	1
1
2
3

Règle du test

Devant chaque ligne et chaque colonne, une instruction permet de déterminer le nombre successifs de cases à noircir. Dans le cas où les instructions sont séparées par un espace, cela signifie qu'il y a au moins une case blanche entre les cases à noircir.

Les instructions sont données pour une ligne de gauche à droite et pour une colonne de haut en bas.

Exemple d'instructions:

1 : il faut noircir une case.

2 : il faut noircir deux cases consécutives.

1 3 : il faut noircir une case, puis après une ou plusieurs cases vides, il faut noircir trois cases consécutives.

2 1 : il faut noircir deux cases consécutives, puis après une ou plusieurs cases vides, il faut noircir une case.

Exemple d'exercices

Exemple 1 : Vous pouvez cocher les cases pour vous entraîner avant de regarder la solution ci-dessous.

	1	1 1	2
3
1
1

Méthode : Première ligne : toutes les cases sont à noircir. Deuxième colonne : 2 cases à noircir avec une case blanche entre les deux, il n'y a qu'une possibilité. Troisième colonne : deux cases successives sont à noircir, il n'y a qu'une possibilité.

	1	1 1	2
3
1
1

Exemple 2 : Vous pouvez cocher les cases pour vous entraîner avant de regarder la solution ci-dessous.

	1 2	1 1	1	1
2 1
1
2
1

Méthode : Première ligne : 2 cases + 1 case à noircir avec une case blanche entre les deux, il n'y a qu'une possibilité. Première colonne : 1 case + 2 cases à noircir avec une case blanche entre les deux, il n'y a qu'une possibilité. Troisième ligne : deux cases successives sont à noircir, il n'y a qu'une possibilité. Deuxième ligne & troisième colonne : 1 case à noircir, il n'y a qu'une possibilité.

	1 2	1 1	1	1
2 1
1
2
1

Méthodologie

Compléter les lignes / colonnes avec une seule possibilité

Exemple 3 cases (ligne) :

1 1
3

Exemple 4 cases (ligne) :

1 2
2 1
4

Exemple 5 cases (ligne) :

1 3
3 1
2 2
5

Compléter les cases avec une seule possibilité

Exemple 3 cases (ligne) :

2
ou 2

La case du milieu sera forcément noircie.

Exemple 4 cases (ligne) :

3
ou 3

Les deux cases du milieu seront forcément noircies.

Exemple 5 cases (ligne) :

2 1
ou 2 1
ou 2 1

La deuxième case sera forcément noircie.

Tester les différentes possibilités

Une fois les cases noircies avec certitude, intéressez-vous aux lignes qui comportent le plus de cases à noircir et essayez les différentes possibilités.

A la fin, vérifiez chaque ligne et chaque colonne afin de vous assurer que vous n'avez pas fait d'erreur. De plus, vérifiez que le nombre de cases noircies correspond bien à la somme des chiffres en haut des colonnes ou à gauche des lignes.

Test des matrices

Le test des matrices, encore appelé test des matrices progressives de Raven, est souvent utilisé comme test d'intelligence dans les cabinets de recrutement ou lors de concours.

Dans ce genre de test, il faut soit compléter une figure avec une partie manquante soit trouver la loi de progression d'une série graphique d'une matrice 2x2 ou 3x3.

Test des matrices - Type 1

Le premier type de test des matrices consiste à déterminer la partie manquante d'une figure parmi plusieurs propositions.

Exemple :

Réponse : 1

Test des matrices - Type 2

Le deuxième type de test des matrices consiste à trouver le raisonnement logique qui unit plusieurs figures géométriques entre elles.

Exemple 1:

Réponse : 1

Exemple 2:

Réponse : 1

Ces tests suivent les mêmes principes que ceux des tests de suites graphiques.

Série graphique

Les tests de suites graphiques utilisent comme support des figures géométriques. Dans ce type de test, il faut trouver la loi de progression des objets afin de déterminer la figure manquante.

Les types de tests de séries graphiques

Il existe plusieurs types de représentation pour ce genre de test.

1er type : Trouver la dernière figure

Exemple 1 - 4 figures :

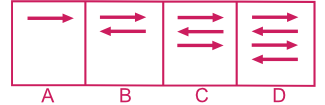
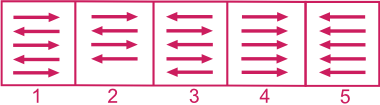Réponse : 1

Exemple 2 - 5 figures : 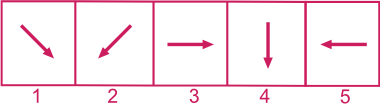Réponse : 1

2ème type : Trouver la figure manquante

Exemple : 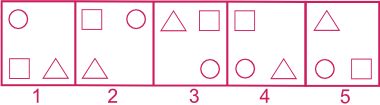Réponse : 1

3ème type : Trouver l'intrus dans la série

Exemple : 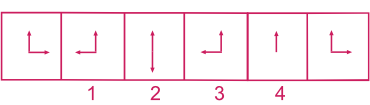Réponse : 1

4ème type : Trouver l'ordre de la série

Exemple : Réponse : 3 4 1 2

Les transformations les plus fréquentes

Déplacement

Déplacement en diagonale

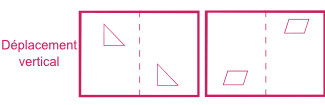
Déplacement vertical (haut en bas ou inversement)

Déplacement horizontal (gauche à droite ou inversement)

Rotation

Rotation de 45° dans le sens horaire

Rotation de 90° dans le sens horaire

Rotation de 135° dans le sens horaire

Rotation de 180°

Rotation de 135° dans le sens anti-horaire

Rotation de 90° dans le sens anti-horaire

Rotation de 45° dans le sens anti-horaire

Symétrie

Symétrie axe vertical

Symétrie axe horizontal

Changement de couleur

Changement de forme

Multiplication du nombre d'éléments

Série lettres & mots

Les suites alphabétiques sont fréquemment utilisées dans les tests de sélection. Il faut retrouver une logique de progression entre des lettres ou des mots afin de compléter la réponse manquante.

Suite de lettres

Pour commencer ce genre de test, il est important de se noter l'alphabet numéroté en ordre croissant et décroissant. En effet, de nombreuses questions utilisent le rang des lettres dans l'alphabet.

A	B	C	D	E	F	G	H	I	J
1 26	2 25	3 24	4 23	5 22	6 21	7 20	8 19	9 18	10 17

K	L	M	N	O	P	Q	R	S	T
11 16	12 15	13 14	14 13	15 12	16 11	17 10	18 9	19 8	20 7

U	V	W	X	Y	Z
21 6	22 5	23 4	24 3	25 2	26 1

A partir du tableau, il devient facile de remplacer les lettres par leur numéro d'ordre et de retrouver la logique de progression.

Exemple : A C E G ? Solution : I.
En remplaçant les lettres par leur chiffre, nous obtenons : 1 3 5 7; nous constatons une suite (+2); la solution est donc 9 soit I.

Séries de références

Certains exercices de suites de lettres utilisent des séries de références, les plus utilisées sont :

- Jours de la semaine : lundi, mardi, mercredi, jeudi, vendredi, samedi, dimanche

- Mois de l'année : Janvier, Février, Mars, Avril, Mai, Juin, Juillet, Août, Septembre, Octobre, Novembre, Décembre

- Nombres : Un, Deux, Trois, Quatre, Cinq, Six, Sept, Huit, Neuf, Dix ...

- Notes de musique : Do, Ré, Mi, Fa, Sol, La, Si, Do

Suite de mots

Le test utilise comme support les mots, sans tenir compte de leurs sens. Pour résoudre ces suites, il faut observer les lettres des mots afin de trouver la logique de l'exercice, notamment le nombre de lettres, de voyelles, de consonnes, mais aussi l'initiale ou la dernière lettre du mot ou encore les majuscules et les minuscules.

Exemple : maison voiture meuble - mAIsOn vOItUrE ?????? Solution: mEUblE, les voyelles sont en majuscules.

La série de mots proposés peut contenir des anagrammes, c'est à dire des mots dont les lettres ont été mélangées.

Exemple : Maison Aimons Tour ?????? Solution: Trou. Anagramme de Tour.

La suite de mots peut être construite à partir de palindromes, c'est à dire de mots dont l'ordre des lettres reste le même qu'on les lise de gauche à droite ou de droite à gauche.

Exemple : rotor anna col??  

Solution: coloc.

Série numérique

Les tests de suites numériques sont fréquemment utilisés lors des tests de sélection. Ils permettent d'évaluer les capacités d'une personne à raisonner avec les chiffres et à calculer mentallement.

Il s'agit d'identifier la logique qui gouverne la séquence afin de déterminer le chiffre manquant en utilisant la plupart du temps les opérations de base (addition, soustraction, multiplication, division). Il arrive aussi que la progression utilise la propritété des nombres (nombres pairs ou impairs, multiples, nombres premiers, ...).

Une opération

Exemple d'une suite arithmétique de progression (+2) : 2 4 6 8 ...
Solution : 2 (+2) 4 (+2) 6 (+2) 8 ...

Exemple d'une suite arithmétique de progression (-2) : 8 6 4 2 ...
Solution : 8 (-2) 6 (-2) 4 (-2) 2 ...

Exemple d'une suite géométrique de progression (x2) : 2 4 8 16 ...
Solution : 2 (x2) 4 (x2) 8 (x2) 16 ...

Exemple d'une suite géométrique de progression (/2) : 16 8 4 2 ...
Solution : 16 (/2) 8 (/2) 4 (/2) 2 ...

Deux opérations

Exemple d'une suite (+2) (+4) : 2 4 8 10 14 ...
Solution : 2 (+2) 4 (+4) 8 (+2) 10 (+4) 14 ...

Exemple d'une suite (+2) (-4) : 2 4 0 2 -2 ...
Solution : 2 (+2) 4 (-4) 0 (+2) 2 (-4) -2 ...

Exemple d'une suite (+2) (x2) : 2 4 8 10 20 ...
Solution : 2 (+2) 4 (x2) 8 (+2) 10 (x2) 20 ...

Trois opérations

Exemple d'une suite (+2) (-3) (x4) : 2 4 1 4 6 3 12 ...
Solution : 2 (+2) 4 (-3) 1 (x4) 4 (+2) 6 (-3) 3 (x4) 12 ...

Opérations groupées

Exemple d'une suite (+1 x2) : 2 6 14 30 ...
Solution : 2 (+1 x2) 6 (+1 x2) 14 (+1 x2) 30 ...

Opérations entre les chiffres

Exemple d'une suite : 1 2 3 5 8 13 21 ...
Solution : 1 2 (1 + 2) 3 (2 + 3) 5 (3 + 5) 8 (5 + 8) 13 (8 + 13) 21 ...

Suites intercallées

Exemple d'une suite : 2 3 4 6 6 9 8 12 10 15 ...
Solution : Suite 1 : 2 (+2) 4 (+2) 6 (+2) 8 (+2) 10 et suite 2 : 3 (+3) 6 (+3) 9 (+3) 12 (+3) 15

Suites symétriques

Exemple d'une suite : 1 2 3 4 5 5 4 3 2 1

Suites particulières

Nombres pairs : 0 2 4 6 8 10 ...

Nombres impairs : 1 3 5 7 9 11 ...

Nombres premiers : 2 3 5 7 11 13 17 19 23 ...

Multiples de 5 : 0 5 10 15 20 25 ...

Suite alpha-numérique

Les tests de suites alphanumériques combinent les suites de chiffres et les suites de lettres en les liant selon différentes règles de logique.

S'il existe un lien entre les chiffres et les lettres, il peut correspondre aux rangs des lettres dans l'alphabet, aux nombres de caractères du mot, aux nombres de voyelles ou de consonnes ou encore à la fréquence d'une lettre dans un mot.